基本介紹
- 中文名:等腰直角三角形
- 外文名:Isosceles triangle
- 寫作:等腰Rt△
- 邊的個數:3
- 內角的個數:3
- 三內角的度數:90°、45°、45°
- 三內角和度數:180°
- 套用學科:數學
概念
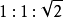
性質
判定
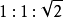



特殊類型



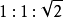
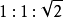





等腰直角三角形是一種特殊的三角形,具有所有三角形的性質:穩定性,兩直角邊相等 直角邊夾一直角銳角45°,斜邊上中線角平分線垂線 三線合一,等腰直角三角形斜邊上的...
等腰直角三角形是一種特殊的三角形,具有所有三角形的性質:穩定性,兩直角邊相等,直角邊夾亦直角銳角45,斜邊上中線垂線,頂角角平分線三線合一,等腰直角三角形斜邊上...
等腰三角形(isosceles triangle),指至少有兩邊相等的三角形,相等的兩個邊稱為這個三角形的腰。等腰三角形中,相等的兩條邊稱為這個三角形的腰,另一邊叫做底邊。兩...
直角三角形是一個幾何圖形,是有一個角為直角的三角形,有普通的直角三角形和等腰直角三角形兩種。其符合勾股定理,具有一些特殊性質和判定方法。...
任意三角形是一個擁有隨意性的三角形,可以是直角三角形,也可以是銳角三角形,更可以是鈍角三角形、等邊三角形、等腰三角形。...
直角三角形是一個幾何圖形,是有一個角為直角的三角形,有普通的直角三角形和等腰直角三角形兩種。其符合勾股定理,具有一些特殊性質和判定方法。[2] 它除了具有一般...
(6)直角三角形的內切圓的半徑r=1/2(AB+AC-BC)(公式一);r=AB*AC/(AB+BC+CA)(公式二)等腰直角三角形三邊之比:1:1:根號二...
在我們現代社會中,三角板(英文set square)是學數學、量角度的主要作圖工具之一。 每副三角板由兩個特殊的直角三角形組成。一個是等腰直角三角板,另一個是特殊角...
麥克斯韋顏色三角形(Maxwell’s color triangle)亦稱“顏色三角”。是顏色標定技術。麥克斯韋最早提出。基本形狀為一等腰直角三角形。三個頂角分別代表紅、綠、藍三種...
三角尺(set square),也稱為三角板,是一種常用的作圖工具。三角尺具有三個角、三個邊, 每副三角尺由兩個特殊的直角三角形組成。一個是等腰直角三角尺,另一個...
三角形按它的內角分類,可分為銳角三角形、直角三角形和鈍角三角形;按它的邊長關係分類,可分為不等邊三角形(三邊兩兩不相等)和等腰三角形(最少有兩邊相等),...
正弦值是在直角三角形中,對邊的長比上斜邊的長的值。 任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值。...
九日多邊形是中國青年數學家王張旭發現並拓展的一種幾何推廣圖形。王張旭於2016年正式編寫該圖形。定義:以任意一個N邊形作為原圖形在每條邊上作等腰直角三角形(該...
橫截面是等腰直角三角形的稜鏡叫全反射稜鏡。...... 圖19-26中的等腰直角三角形ABC表示一個全反射稜鏡的橫截面,它的兩個直角邊AB和BC表示稜鏡上兩個互相垂直的...
把兩條對角線的數量關係和位置關係集中到一個三角形中,將求梯形上下底的長轉化為求直角三角形斜邊的長 例6、如圖,在等腰梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,...
泛指事物的分支或一部分,中國古代稱不等腰三角形構成直角的較長的邊。也作量詞。 中文名 股 拼音 gǔ 總筆畫 8 部首 月 目錄 1 基本資料 2 漢字演變 ...
