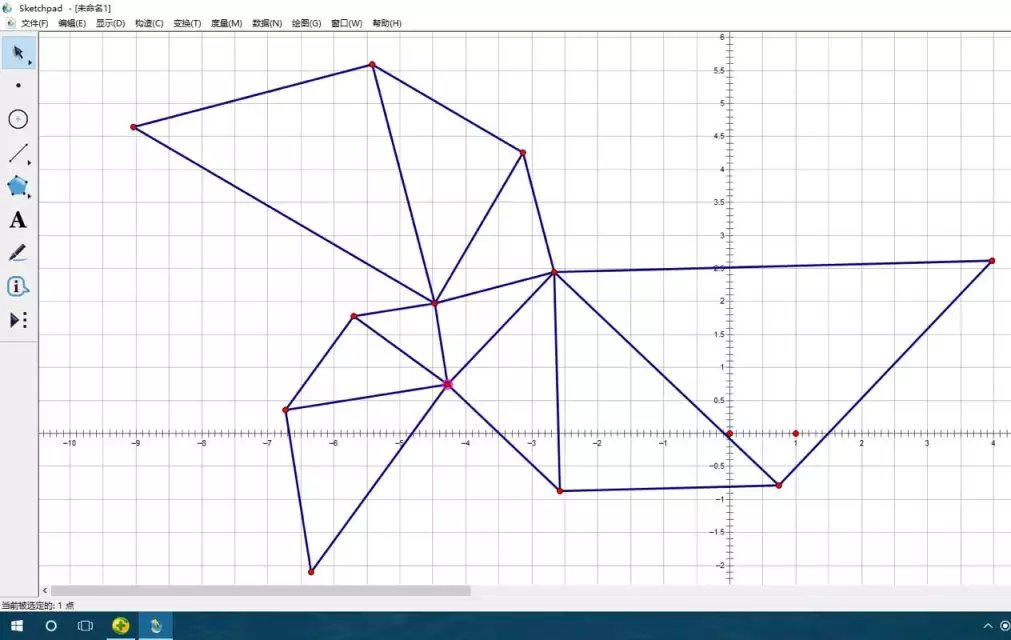
九日多邊形是中國青年數學家王張旭發現並拓展的一種幾何推廣圖形。王張旭於2016年正式編寫該圖形。
定義:以任意一個N邊形作為原圖形在每條邊上作等腰直角三角形(該條邊為三角形的一條腰),但作的每個等腰直角三角形的垂足不能相交。這樣得到的圖形是一階圖形。再把外層的每一個等腰直角三角形的斜邊的最外一個頂點當成垂足作等腰直角三角形,這樣就得到了二階圖形。以此內推,當等腰直角三角形剛好重疊,就得到了一個完整的九日多邊形。每個重疊而重合的角稱為契合角,契合角度數相加就是契合總角度。
基本介紹
- 中文名:王張旭多邊形(九日多邊形)
- 外文名:jiu ri polygon
- 發現者:王張旭
- 運用範圍:建築學、解析幾何
中國青年數學家王張旭發現九日多邊形。
該圖形簡潔明了,可以以生活中任意的有邊有棱的東西作九日多邊形。在一段時間內該圖形使王張旭本人沉迷,他認為該圖形是世界上最美的圖形,堪比泰森多邊形。
定義:以任意一個N邊形作為原圖形在每條邊上作等腰直角三角形(該條邊為三角形的一條腰),該等腰直角三角形稱為延伸三角,但作的每個等腰直角三角形的垂足不能相交。這樣得到的圖形是一階圖形。再把外層的每一個等腰直角三角形的斜邊的最外一個頂點當成垂足作等腰直角三角形,這樣就得到了二階圖形。以此內推,當等腰直角三角形剛好重疊,就得到了一個完整的九日多邊形。每個重疊而重合的角稱為契合角,契合角度數相加就是契合總角度。
性質:
1.以三邊形為原圖形可作14個延伸等腰直角三角形。因為(360*3-180-90*3)÷45=14。且原圖形是等腰直角三角形時無契合角,剛好重合,是完美契合。
推廣:以N邊形為原圖形時可作2N+8個延伸三角,可見成等比關係。
2.每層的每個延伸三角的外層頂點兩兩相連會形成一個N邊形(稱為復圖形),該N邊形與原N邊形成相似關係。
3. 每一層的復圖形的面積成等比關係
4.三邊形的契合總角為45°(原圖形為等腰直角三角形時完美契合)、四邊形的契合總角為90°(矩形時完美契合)
推廣:N邊形的契合總角為45°(N-2),若且唯若原圖形為等腰直角三角形和矩形時沒有契合角,稱為完美契合。九日多邊形實際上可以運用於建築學。王張旭又提出曲面九日多邊形和新的曲面曲程度的相關理論。