軸對稱圖形是指一條軸線的兩邊完全對稱的圖形,形狀都完全對稱。
基本介紹
- 中文名:什麼是軸對稱圖形
- 外文名:axial symmetric figure
- 舉例:正方形
- 領域:數學
定義
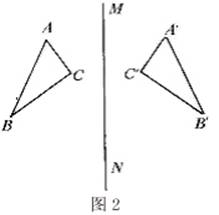 軸對稱圖形
軸對稱圖形 軸對稱圖形2 示例
軸對稱圖形2 示例性質
 軸對稱圖形2 示例
軸對稱圖形2 示例定理及逆定理
繪製方法
方法
畫法
 蝴蝶也是一種軸對稱圖形
蝴蝶也是一種軸對稱圖形
軸對稱圖形是指一條軸線的兩邊完全對稱的圖形,形狀都完全對稱。
 軸對稱圖形
軸對稱圖形 軸對稱圖形2 示例
軸對稱圖形2 示例 軸對稱圖形2 示例
軸對稱圖形2 示例 蝴蝶也是一種軸對稱圖形
蝴蝶也是一種軸對稱圖形軸對稱圖形是指一條軸線的兩邊完全對稱的圖形,包括顏色與形狀都完全對稱。... 什麼是軸對稱圖形 軸對稱圖形是指一條軸線的兩邊完全對稱的圖形,包括顏色與形狀都完全...
軸對稱圖形(axial symmetric figure),數學術語,定義為平面內,一個圖形沿一條直線摺疊,直線兩旁的部分能夠完全重合的圖形。直線叫做對稱軸(axis of symmetric),並且...
對稱圖形有很多分類,例如軸對稱圖形:如果一個圖形沿著一條直線對摺後兩部分完全重合,這樣的圖形叫做軸對稱圖形。如果一個圖形繞某一點旋轉180度,旋轉後的圖形能和...
如果一個平面圖形沿著一條直線摺疊後,直線兩旁的部分能夠互相重合,那么這個圖形叫做軸對稱圖形(a figure has reflectional symmetry),這條直線叫做對稱軸(axis of ...
使幾何圖形成軸對稱或旋轉對稱的直線。對稱圖形的一部分繞它旋轉一定的角度後,就與另一部分重合。 許多圖形都有對稱軸。例如橢圓、雙曲線有兩條對稱軸,拋物線有一...
面對稱空間圖形(space figure symmetric with respect to a plane)是一種特殊的圖形,指空間圖形以一個鏡面反射變換為其自對稱變換的圖形。鏡面反射變換的反射面稱...
對稱多面角是兩個特殊相關的多面角,互為中心對稱、軸對稱、鏡面對稱的多面角的統稱。兩多面角中,如果一個是另一個的中心對稱圖形、軸對稱圖形、鏡面對稱圖形,則分...
③、由一個圖形變為另一個圖形,並使這兩個圖形關於某一條直線成對稱軸,這樣的圖形改變叫做圖形的軸對稱變換,也叫反射變換,簡稱反射。經變換所得的新圖形叫做原...
植物莖蔓的手性纏繞是由什麼決定的?同種植物是否可能具有不同的手性? 左右對稱...既不是軸對稱圖形又不是中心對稱圖形:不等腰三角形,直角梯形,普通四邊形...
圖形對稱是一款由Applusoft Limited於2012-11-6開發的一款休閒遊戲。...... 而您的任務便是要從這堆圖形部件中找出可合併成對稱圖形的部件,並將其合併。一個對稱...
把一個圖形繞著某一個點旋轉180°,如果它能夠與另...植物莖蔓的手性纏繞是由什麼決定的?同種植物是否...面、對稱中心、對稱軸、旋轉反伸軸和旋轉反映軸。...
《左右對稱剪紙》是2005-05-01 浙江科學技術出版社出版的一本圖書 ...左右對稱剪紙》是介紹的是左右對稱剪紙,而且僅限於單個物體的對稱圖形。內容分蔬果...
也稱“Bilateral Ambigram”,即軸對稱字。如果在字母旁豎起一面鏡子,那么它在...倒轉180度後,與原圖形完全一樣,仍然可以清晰地讀出四個單詞的字樣! ...
對稱又稱“均齊”,是在統一中求變化;平衡則側重在變化中求統一。兩者綜合套用,就產生的平衡的三種形式:對稱平衡、散射平衡和非對稱平衡。對稱的圖形具有單純、簡潔...
