定義
定義一
平面上若干條線段順次首尾相接(每條最多同另外兩條聯結且端點不在另外線段內部)構成的圖形,稱為(平面)折線;如折線每邊都有兩鄰邊,就叫(封)閉折線,否則,叫開折線.這樣就可對摺線進行初步的分類和對幾個常用概念給予明確的界定:邊不相交的折線為簡單折線,簡單閉折線叫作多邊形。多邊形劃分平面為兩部分,有限部分叫內部,無限部分叫外部。用歸納法易證:n邊形內部可用不相交對角線,劃分為以其頂點為頂點的互不重疊的n一2個三角形,從而可直接推出內角和定理。且可提出如下幾個方面的問題(以下問題更多內容請參考相應參考文獻):
(1)
折線整體性質的研究:
拓撲和其他結構特徵、複雜性指標、組合計數問題、合成與分拆、有關
度量性質研究等;
(2)特殊折線的研究:如直角折線、等角或等邊折線、平行多邊折線、具有某種特徵的折線(短程線、遍歷折線)的存在和構造問題;
(3)圓與凸多邊形內接折線(如星形折線)的研究等。
定義二
折線是一種幾何圖形,指不全在同一直線上的幾條線段順次首尾相接組成的圖形(如圖1,圖2)。各線段稱為折線的邊或折線的節;折線各邊長之和稱為折線的長;各線段的端點稱為折線的頂點;相鄰兩個頂點稱為鄰頂點;不是兩條線段公共端點的兩個頂點都稱為折線的端點;兩端點重合(實際上即無端點)的折線稱為封閉折線(圖2);組成折線的所有線段都在同一平面內的折線稱為平面折線,否則稱為空間折線;凡不相鄰的兩邊不相交的折線稱為簡單折線;把一條平面簡單折線的任一條邊向兩方延長成直線,如果能使這條折線的其他各邊都在這條直線的同側,那么這條平面折線稱為凸折線;連結非封閉折線的兩個端點的線段稱為折線的鎖線。
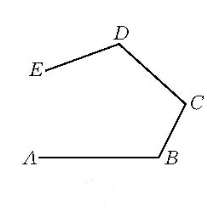 圖1
圖1 圖2
圖2定義三
在同一平面上, 由不在同一條直線上的幾條線段,順次首尾相接組成的圖形。如圖中的ABCDE和PQRSTP都是折線。折線的起點和終點稱為端點,如果一條折線的兩個端點重合,這條折線叫做封閉折線。如圖中折線PQRSTP為封閉折線。
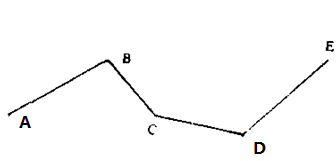 圖3
圖3 圖4
圖4特徵性質
為了弄清折線的特徵性質,觀察圖5,看閉折線
的邊
,
,
,
,它們的鄰邊折向有不同的情況(圖6):
:和
的兩鄰邊都折向異側,而
和
兩鄰邊折向同側,前者叫雙摺邊,後者叫單折邊。雙摺邊又有不同:如在
鄰邊加上向外的力,它會向右旋轉故稱右旋邊,類似地
稱為左旋邊,這種由於在頂點“拐彎”而形成的邊的折性確實是折線的特徵性質,這由如下命題即可知曉。
 圖5
圖5 圖6
圖6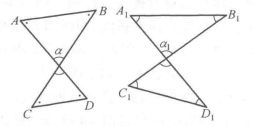 圖7
圖7命題1(折線特徵性質) 閉折線如有雙摺邊則必有偶數條,左右旋邊各半且相間排列。
比如,在
處左拐,則在
處必須右拐,才能使
為雙摺邊(右旋邊)。如要生成下一條雙摺邊,又必須在某處,比如
處左拐,從而使
成為左旋邊。因此命題似乎成立,但證來頗不易,直到發現了邊的“雙標號”法才給出了證明,如稱頂點處劣角為頂角,則知有:
命題2 有雙摺邊的閉折線,頂角和不定。
如圖7所示的“蝶形”,其頂角和
但這種蝶形有一個優良性質,即
,這是求折線頂角和的一個“轉移”工具。
由兩個命題可推出一系列重要事實,如奇數條邊的封閉折線至少有一條單折邊、
多邊形為凸的
充要條件是無雙摺邊,等,且一眼可看出很多折線的規律性。
如圖8所示的開折線中:(a)是回形折線,無雙摺邊;
(b)為齒形折線,單雙相間;
(c)為階形折線,無單折邊。
 圖8
圖8而且可看出如圖9所示的兩種星形中的(a)是回式星形,全由單折邊構成;(b)為階式星形,全由雙摺邊構成,且知前者頂角和為
,後者頂角和不確定。
 圖9
圖9 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4

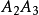

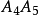

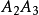

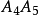

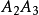
 圖5
圖5 圖6
圖6 圖7
圖7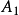
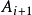


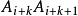
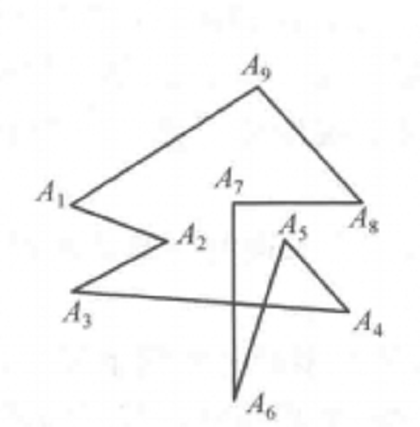
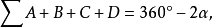

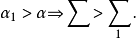
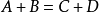
 圖8
圖8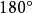
 圖9
圖9