基本介紹
- 中文名:調和測度
- 外文名:harmonic measure
- 所屬學科:數學
- 所屬問題:複變函數論(調和函式)
- 相關概念:狄利克雷問題、測度、若爾當弧等
- 符號:ω(z,α,D)
定義








基本性質



















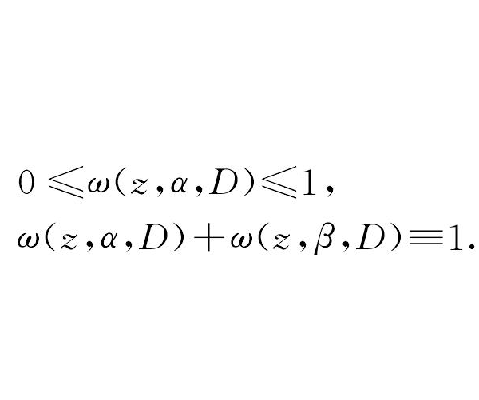



























調和測度(harmonic measure)是特殊的狄利克雷問題的解,是邊界點集的一種測度。設D為一個區域,其邊界∂D由有限條若爾當弧組成,∂D分為α和β兩部分,則在D記憶體在惟一的一個有界調和函式u(z)在α上取邊值1,...
μ上調和測度 μ上調和測度伽(-superharmonic measure)通常的上調和函式在群上位勢論中的對應物。若ED+ ,則稱寧是產上調和測度<調和測度.哈爾測度wx是產上調和測度.若且唯若爪(X)=1時,wx是f調和測度.
調和測度:幾何與分析的觀點(影印版)《調和測度:幾何與分析的觀點(影印版)》是高等教育出版社出版的圖書,作者是Luca Capogna、Carlos E. Kenig、Loredana Lanzani。
主要理論問題有:邊界為分形的區域上的調和測度的分析與幾何性質;分形集合或曲線的Martin邊界;具有分形邊界或分形支撐的位勢和解析函式的奇異邊界增長性質,特別是它們與重分形的內在聯繫;相關代換序列的動力系統或分形性態;利用分形或重...
是V的U調和測度),那么u稱為U上的(相對於H的)局部超調和函式,記 為U上的局部超調和函式全體,則 是X上的超調和簇,稱為由H產生的超調和簇,並且,H就是與 相關的調和簇。相關定理 引理1 設 是Brelot調和空間,G為區...
harmonic measure [數] 調和測度 ; 低測度 administrative measure [管理] 行政措施 ; 行政辦法 ; 行政處分 Radon measure 拉東測度 ; 拉冬測度 ; Radon測度 Gibbs measure 吉布斯測度 technical measure 技術措施 Measure Tape 拉尺發條...
接受狀態的論文一篇 我們考慮球單位面上的調和測度,此測度依賴於出發點x和維數n。其被證明具有一致的gauss型集中現象,等價於L1的傳輸不等式常數具有1/n的階,與x無關。與Barthe和張正良合作,我們利用球面上調和測度只依賴於一個變數...
它們不但反映常返和暫留的性質,與調和測度有密切的聯繫,而且與可加范函的Balayage以及平衡測度有重要的聯繫.本項目主要研究馬氏過程的首離時和首離點的分布以及末離時和末離點的分布,分析被可乘范函Killing後和時間變換後的首離時和...
該項目主要研究機率論中的幾個泛函不等式,這其中包括亞橢圓運算元的泛函不等式,隨機微分方程,如反映擴散方程,滯後系統,Burgers方程,Navier-Stokes方程等軌道空間上的泛函不等式以及一些含參變數的具有實際意義的測度和分布,如調和測度,...
相等且只取有限值時,廣義狄利克雷問題有解,即 f 是可解的。f 可解的充分必要條件是對每個x∈D,f 關於調和測度 可積分,這時 就是所要求的惟一解,稱為PWB解或PB解,以紀念佩龍、維納(Wiener,N.)及布雷洛的工作。特別...
關於n維歐式空間中球面旋轉不變測度的龐加萊不等式,得到了n/n-1倍的上下界估計。以及一維相應情形的精確估計。關於球面上的測度的泛函不等式:球面上Moebius測度的龐加萊與對數Sobolev不等式;球面上調和測度的Sobolev不等式;球面上推廣...
17.1 調和測度 17.2 Brown 運動和共形變換 17.3 最大雙曲圓盤填充 17.4 組合單值化定理 17.5 機率解釋 第三部分曲面論和幾何逼近論 第十八章曲面論 18.1 曲面的標架和活動標架法 18.2 曲面的微分式及其幾何 18.3 曲面的...
第六章調和函式與dirichlet 問題 1 調和函式及次調和函式 1.1 調和函式及其序列 1.2 次調和函式 2 dirichlet 問題與調和測度 2.1 dirichlet 問題 2.2 green 函式 2.3 調和測度 第七章г函式和b 函式 1 г函式 1.1 г(z) ...
全純Mobius變換在信號分析中的套用來自於全純Mobius變換的邊值, 它誘導出調和測度和非線性Fourier原子,產生了信號分析中具有遞次濾波的新濾波器, 也產生了具有非等距離採樣點的Shannon型採樣定理。 非線性 Fourier原子理論拓廣了全純Har...
本項目研究了擬極值距離常數、擬對稱指數、由區域誘導的單位圓周上的縫契約胚、調和測度、調和對稱等相關問題。在高維歐式空間中,證明了擬極值距離常數或者被非蛻化的連續統達到,或者有1+H的上界。同時還證明了高維歐式空間中的容量所...
作為特例,在李普希茨區域內的上調和函式u>0在∂D上除一個調和測度零集外處處有細邊界值。細邊界值 細邊界值是函式在細拓撲意義下的邊界值。一般地,若x從D趨於x₀(x₀∈∂D)時有f(x)→α,則稱α為f在x₀的邊界值...
1具有均值性質的函式 151 7.3.2 Harnack原理151 7.3.3次調和函式 152 7.3.4 Dirichlet問題的解 154 7.4多連通區域的典範映射 156 7.4.1調和測度156 7.4.2 Green函式158 7.4.3平行割線區域 160 習題 7 160 索引162
其他成就包括創立了調和測度與相伴原理,以及哈達馬三圓定理的推廣、彈道的測定等。奈望林納一生在許多不同論題上不斷地寫了大量的文章與書,寫有名著《解析函式論》(1936,有多種文字譯本)、《皮卡-波萊爾定理與亞純函式理論》(1929)...
42 分形測度及其奇異性?理論框架 43 精確可解的康托集 44 動力系統 45 滲流集團上的電阻網路 46 DLA生長機率測度?調和測度 47 生長結構的幾何多重分形性 48 多重分形的熱力學形式 49 楊-李零點?朱莉亞集和它們的奇異譜 第7章 ...
(6)研究了關於具有Poisson測度的排隊模型的泛函不等式。對於具有Gibbs測度的Glauber動力系統,我們在Dorbrushin條件下得到了相應的泛函不等式。(7)對於球上的調和測度,我們得到了相應的對數sobolev不等式和poincare不等式。
