基本介紹
- 中文名:廣義狄利克雷問題
- 外文名:generalized Dirichlet problem
- 類型:經典狄利克雷問題的推廣
- 相關:調和函式
- 一級學科:數學
- 二級學科:位勢論
















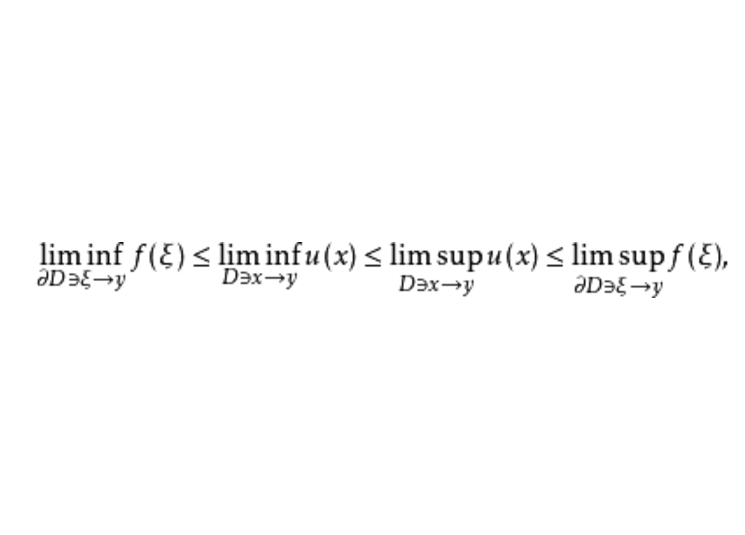
















廣義狄利克雷問題(generalized Dirichlet problem)是經典狄利克雷問題通過適當放鬆邊界值要求進行的推廣。而經典狄利克雷問題也叫做第一邊值問題,是經典位勢論中三大...
在數學中,狄利克雷邊界條件,為常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。求出這樣的方程的解的問題被稱為狄利克雷問題。狄利克雷問題(...
數學中,經典狄利克雷問題(classical Dirichlet problem)是尋找一個函式,使其為給定區域內一個指定的偏微分方程(PDE)的解,且在邊界上取預定值。
例如,著名的圓或橢圓內的整點問題,球或橢球內的整點問題,以及除數問題等。高斯和狄利克雷(Dirichlet,P.G.L.)分別在“圓內整點問題”和“除數問題”的研究中...
在廣義狄利克雷級數的表達式中:若令a0=0,μ0=0,μn=log n(n=1,2,3,...),則得到狄利克雷級數。中文名 廣義狄利克雷級數 外文名 generalized DeLickley...
所謂正則邊界點,是指Rn(n≥2)的一個開集ω的邊界點x0,使得以∂ω上每個具有緊支集的連續函式f為邊界值的廣義狄利克雷問題的解在x0的邊界值與f(x0)一致...
合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 廣義狄利克雷乘積編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關內容使...
狄利克雷原則是德國數學家狄利克雷首先明確的提出來並用以證明一些數論中的問題,也稱為狄利克雷原則。...
狄利克雷分布(Dirichlet distribution)或多元Beta分布(multivariate Beta distribution)是一類在實數域以正單純形(standard simplex)為支撐集(support)的高維連續機率分布...
狄利克雷邊界條件,常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。...
在數學中,狄利克雷原理(Dirichlet principle)是將求解拉普拉斯方程狄利克雷問題化為變分問題的方法,所用到的積分稱為狄利克雷積分。狄利克雷原理古典形式稱,在∂G...
狄利克雷函式(英語:dirichlet function)是一個定義在實數範圍上、值域不連續的函式。狄利克雷函式的圖像以Y軸為對稱軸,是一個偶函式,它處處不連續,處處極限不存在...
1850年發表了有關位勢理論的文章,論及著名的第一邊界值問題,現稱狄利克雷問題。 [3] 狄利克雷是19世紀最重要的數學家之一。他的貢獻涉及到數學的各個方面,...
狄狄利克雷級數在解析數論中有重要的地位。黎曼ζ函式和狄利克雷L函式都可以用狄利克雷級數來定義。有猜測所有的狄利克雷級數組成塞爾伯格類函式都滿足廣義黎曼猜想。
狄利克雷區域編輯 鎖定 討論 本詞條由“科普中國”科學百科詞條編寫與套用工作項目 審核。狄利克雷區域是一類特殊區域。對於狄利克雷問題是可解的域D,稱為狄利克...
1850年發表了有關位勢理論的文章,論及著名的第一邊界值問題,現稱狄利克雷問題。 [4] 詞條圖冊 更多圖冊 參考資料 1. Bartle, Robert G. (10 June 1996)....
這一性質是狄利克雷L函式與黎曼ζ函式的一個主要差別。研究對應於實特徵的L函式的實零點,是L函式論的最重要問題之一。 ? A. 佩奇於1935年證明了:存在絕對正常...
對馬丁邊界同樣可考慮狄利克雷問題;可把Ω上的細拓撲延拓成Ω∪Δ1上的極小細拓撲並可討論函式的邊界值問題;馬丁邊界可翻譯成機率語言並在隨機過程論中得到套用...
例如考慮泊松方程的狄利克雷向題如果存在一個函式 ( 表示函式絕對值的p次方在勒貝格積分的意義下可積的函式類),對於所有的 都有 則稱u為原定解問題的L'-弱解...
並稱之為𝒰-廣義狄利克雷問題的解。 [1] 如果任何φ∈Cc(∂U)(∂U上具有緊支集的連續的實函式全體)都是可解的,則U稱為𝒰可解集,簡稱可解集。可...
所謂正則邊界點,是指Rn(n≥2)的一個開集ω的邊界點x0,使得以∂ω上每個具有緊支集的連續函式f為邊界值的廣義狄利克雷問題的解在x0的邊界值與f(x0)一致...
所謂正則邊界點,是指Rn(n≥2)的一個開集ω的邊界點x0,使得以∂ω上每個具有緊支集的連續函式f為邊界值的廣義狄利克雷問題的解在x0的邊界值與f(x0)一致...
所謂正則邊界點,是指Rn(n≥2)的一個開集ω的邊界點x0,使得以∂ω上每個具有緊支集的連續函式f為邊界值的廣義狄利克雷問題的解在x0的邊界值與f(x0)一致...
對於給定連續邊值函式的狄利克雷問題,得出了確切的廣義群。對於一般的緊集定義容度概念,並給出著名的正則性判據。早先關於一個區域內部的電磁勢的概念認為,它應當...
可解集是使其上𝒰-廣義狄利克雷問題可解的MP集。設U是MP集,φ是從∂U到[-∞,+∞]的函式,把U(𝒰)中滿足下麵條件的u稱為𝒰-上函式:u有下界,存在...
