正則邊界點

正則邊界點(regular boundary point)是一類邊界點。所謂正則邊界點，是指Rⁿ(n≥2)的一個開集ω的邊界點x₀，使得以∂ω上每個具有緊支集的連續函式f為邊界值的廣義狄利克雷問題的解在x₀的邊界值與f(x₀)一致，這等價於Rⁿ\ω(或∂ω)在x₀不瘦，當n≥3時，這等價於x₀為Rⁿ\ω(或∂ω)的2正則點(參見“α正則點”)，故可採用維納判別法(當n=2時，用對數容量代替C_α的類似判別法)。常用的充分必要判別法還有：1.在x₀存在閘函式，即存在x₀的開鄰域N及N∩ω內的上調和函式w>0，使得當x→x₀時w(x)>0；2.對1.中N∩ω的格林函式G有：當x→x₀時，G(x，y)=0。另外，當n≥3時，簡單實用的充分判別法是所謂龐加萊錐條件，即存在以x₀為頂點的圓錐體在x₀的某鄰域與ω不相交。

基本介紹

• 中文名：正則邊界點
• 外文名：regular boundary point
• 所屬學科：數學
• 屬性：一種邊界點
• 相關問題：雙邊生滅過程，數值特徵等

定義

如果狀態空間由所有的整數組成，且矩陣具有下面的形式

則稱矩陣Q為雙邊生滅矩陣，稱Q過程為雙邊生滅過程。下面介紹中，Q總是指雙邊生滅矩陣，Q是保守的，雙邊生滅過程必滿足向後方程組。

對於形如(1)的矩陣Q，令稱

稱為自然尺度，稱

為邊界點。令

稱為標準測度。

令

根據Q，可以將邊界點分類。稱：

為正則，如有限且；

為流出，如有限，且和；

為流入，如無限，且；

為自然，如為剩下的情形。

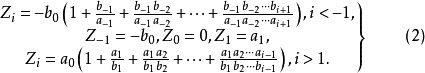
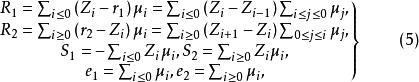
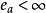
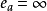
定理

定理正則等價於且；

流出等價於且；

流入等價於且；

自然等價於且。