可解集（resolutive set）是使其上𝒰-廣義狄利克雷問題可解的MP集。
基本介紹
- 中文名：可解集
- 外文名：resolutive set
- 適用範圍：數理科學
簡介,MP集,廣義狄利克雷問題,
簡介
可解集是使其上𝒰-廣義狄利克雷問題可解的MP集。
設U是MP集，φ是從∂U到[-∞,+∞]的函式，把U(𝒰)中滿足下麵條件的u稱為𝒰-上函式：u有下界，存在緊集K，使在U\K上u≥0且對任何ξ∈∂U，當x→ξ時有lim inf u(x)>φ(ξ)。
上函式全體記為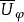
，令
，其中元素稱為𝒰下函式。又記
。如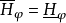
且屬於ℋ𝒰(U)（ℋ𝒰是與𝒰相關的調和簇），那么稱φ（在U上相對於𝒰）可解，這時記
並稱之為𝒰-廣義狄利克雷問題的解。
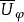
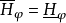
如果任何φ∈Cc(∂U)（∂U上具有緊支集的連續的實函式全體）都是可解的，則U稱為𝒰可解集，簡稱可解集。
MP集
MP集是使某種形式的極小值原理成立的開集。
設X是局部緊的豪斯多夫空間，𝒰是X上的超調和簇，U是開集。若對f∈𝒰(U)，存在緊集K使得在U\K上f≥0，並且∀ξ∈∂U，當x→ξ時lim inf f(x)≥0，則在U上f≥0，那么稱U為MP集。
廣義狄利克雷問題
(generalized Dirichlet problem)
廣義狄利克雷問題是經典狄利克雷問題通過適當放鬆邊界值要求進行的推廣。
該問題是：已知Rn(n≥2)的區域D(∂D為緊)及從∂D到[-∞，+∞]的函式 f，求D內調和的函式u，使對每個正則邊界點y，有
且當D無界時，u在∞為正則(若不要求內外部問題互相轉化，可只要求u在∞有有限極限)。更一般地，可考慮D為一般開集的情形。
