基本介紹
- 中文名：鬆弛問題
- 外文名：slack problem
- 領域：運籌學
- 範疇：整數規劃
- 性質：不考慮整數條件
- 相關名詞：分枝定界法
簡介,整數規劃數學模型,鬆弛問題的一般形式,分支定界法,解的特點,用分枝定界法來解鬆弛問題,舉例,例1,例2,
簡介
要求一部分或全部決策變數必須取整數值的規劃問題稱為整數規劃（integerprogramming，簡記IP）。不考慮整數條件，由余下的目標函式和約束條件構成的規劃問題稱為該整數規劃問題的鬆弛問題（slackproblem）。若鬆弛問題是一個線性規劃，則稱該整數規劃為整數線性規劃（integerlinear programming）。
整數規劃數學模型
鬆弛問題的一般形式
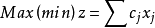
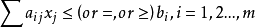
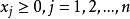
不考慮整數條件，由余下的目標函式和約束條件構成的規劃問題稱為該整數規劃問題的鬆弛問題。
相關結論：
（1）最優解不一定在頂點上達到；
（2）最優解不一定是鬆弛問題最優解的鄰近整數解；
（3）整數可行解遠多餘於頂點，枚舉法不可取。
分支定界法
設有最大化的整數規劃問題A，與它相應的線性規劃問題為B，求解問題B，若B的最優解不符合A的整數條件，則B的最優值一定為A最優值Z*的上界，而A的任意可行解的目標函式值將是Z*的下界，分支定界法就是將B的可行域分成子區域（稱為分支方法）的方法，通過減小最優值的上界和下界最終得到最優值。
分枝定界法求解問題的步驟：
將要求解的整數規劃問題稱為問題A，將其鬆弛問題稱為問題B，若
（1）B沒有可行解，這時A也沒有可行解，停止；
（2）B有最優解，並符合問題A的整數條件，B的最優解即為A的最優解；
（3）B有最優解，但不符合A的整數條件，記它目標函式值為最優值上界。
解的特點
鬆弛問題作為一個線性規劃問題，其可行解的集合是一個凸集，任意兩個可行解的凸組合仍為可行解。
整數規劃問題的可行解是它鬆弛問題可行解集合的一個子集，任意兩個可行解的凸組合不一定滿足整數約束條件，因而不一定仍為可行解。由於整數規劃問題的可行解一定也是它的鬆弛問題的可行解（反之則不一定），所以，前者最優解的目標函式值不會優於後者最優解的目標函式值，即鬆弛問題的最優解是整數規劃問題最優解的上限。
在一般情況下，鬆弛問題的最優解不會剛好滿足變數的整數約束條件，因而不是整數規劃的可行解，自然就不是整數規劃的最優解。此時，若對鬆弛問題的這個最優解中不符合整數要求的分量簡單地取整，所得到的解不一定是整數規劃問題的最優解，甚至也不一定是整數規劃問題的可行解。
用分枝定界法來解鬆弛問題
1、在全部可行性域上解鬆弛問題
若鬆弛問題最優解為整數解，則其也是整數規劃的最優解；
2、分枝過程
（1）若鬆弛問題最優解中某個
不是整數，令
為
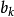的整數部分
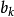
（2）構造兩個新的約束條件
和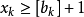
，分別加於原鬆弛問題，形成兩個新的整數規劃；
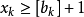
3、求解分枝的鬆弛問題 — 定界過程
設兩個分枝的鬆弛問題分別為問題1和問題2，它們的最優解有如下情況：
序號 | 問題1 | 問題2 | 說明 |
1 | 無可行解 | 無可行解 | 整數規劃無可行解 |
2 | 無可行解 | 整數解 | 問題2的整數解為最優解 |
3 | 無可行解 | 非整數最優解 | 對問題2進行分支 |
4 | 整數解 | 整數解 | 較優解為最優解 |
5 | 整數解，目標函式 優於問題2 | 非整數解 | 問題1的整數解為最優解 |
6 | 整數解 | 非整數解，目標函式 優於問題1 | 對問題1剪枝，其整數解為界，對問題2繼續分支 |
情況 2, 4, 5 找到最優解；
情況 3 在縮減的域上繼續分枝定界法；
情況 6 問題1的整數解作為界被保留，用於以後與問題2的後續分枝所得到的解進行比較，結論如情況 4 或 5。
計算過程可利用靈敏度分析（增加約束條件），簡化問題的計算量。
舉例
例1
試用分枝定界法求解下面整數規劃問題的解：
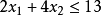
解：鬆弛問題的最優解為
，由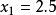
得到兩個分枝如下：
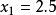
問題1：
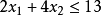
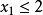
問題2：
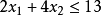
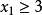
分枝問題的鬆弛解：
問題1 | 問題2 | |
x1 | 2 | 3 |
x1 | 4/9 | 1 |
f(x) | 21 | 22 |
例2
如圖所示，則該整數規劃鬆弛問題的解為：
若繼續為原問題增加兩個條件：
；
則
