線性映射矩陣

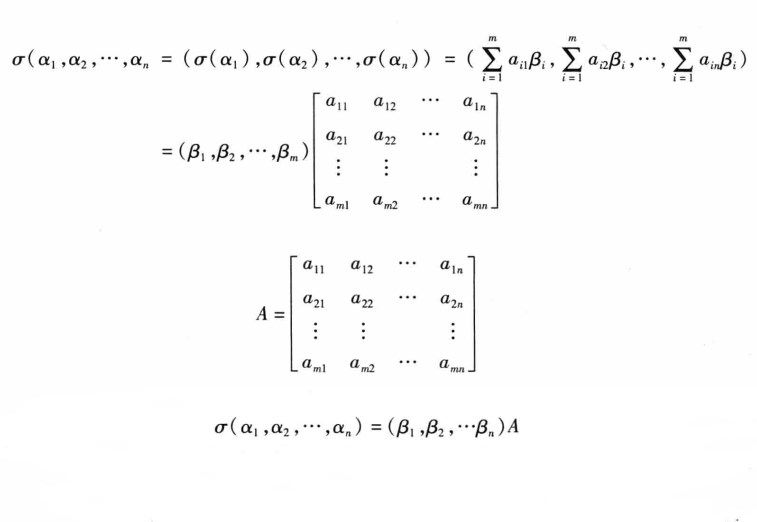
線性映射矩陣(matrix of a linear mapping)是一種特殊矩陣，指線性映射的數量表示。設σ是數域P上n維線性空間V到P上m維線性空間W的一個線性映射，v₁，v₂，…，v_n是V的基，w₁，w₂，…，w_m是W的基。若(σ(v₁)，σ(v₂)，…，σ(v_n))=(w₁，w₂，…，w_m)(a_ij)_m×n，則矩陣(a_ij)稱為σ關於基偶(v₁，v₂，…，v_n)，(w₁，w₂，…，w_m)的矩陣。設V的基變換為(v₁′，v₂′，…，v_n′)=(v₁，v₂，…，v_n)R，W的基變換為(w₁′，w₂′，…，w_m′)=(w₁，w₂，…，w_m)Q，則線性映射σ關於基偶(v₁′，v₂′，…，v_n′)，(w₁′，w₂′，…，w_m′)的矩陣(a_ij′)與(a_ij)是等價的，即(aij′)=Q(a_ij)R.若W=V，則線性變換σ對基v₁，v₂，…，v_n的矩陣(a_ij)與對基v₁′，v₂′，…，v_n′的矩陣(a_ij′)是相似的，即(a_ij′)=R(a_ij)R，其中(v₁′，v₂′，…，v_n′)=(v₁，v₂，…，v_n)R。

基本介紹

• 中文名：線性映射矩陣
• 外文名：matrix of a linear mapping
• 所屬學科：數學
• 所屬問題：高等代數(線性變換)
• 簡介：指線性映射的數量表示

基本介紹

設是V₁的一組基，是V₂的一組基。是的一個線性映射，則

或寫成

把它代入式（1）得

矩陣A稱為線性映射σ在基()與()下的矩陣表示。

有了線性映射(在一對基下)的矩陣表示現在可以解決V₁中向量α與它在V₂中的像之間的坐標關係。

設α∈V，故

它的像σ(α)∈V₂，可寫成

根據σ(α)坐標唯一性，得

寫成矩陣形式

式(4)稱為線性映射在給定基()與()下向量坐標變換公式(原像與像的坐標關係)。

相關定理

線性映射σ在給定基下的矩陣表示A是唯一的，它的逆問題就是下述定理。

定理1 設V₁的基為，V₂的基為，已給m×n矩陣，則存在唯一的線性映射σ，它在這兩個基下的矩陣表示為A。

在指定了空間V₁和V₂的基之後，便可以求得線性映射在指定一對基下的矩陣表示。但是空間基是不唯一的，線性映射在不同對基下的矩陣表示之間有如下關係。

定理2 設σ是的一個線性映射，與是V₁的兩組基，其過渡矩陣為與是V₂的兩組基，其過渡矩陣為Q。線性映射σ在基與下的矩陣表示為A，在基與下的矩陣表示為B，則