坐標變換公式(formula of a coordinates transformation)是線性空間的向量關於不同基的坐標之間的關係式,是解析幾何中(不變原點的)坐標變換公式的推廣。
基本介紹
- 中文名:坐標變換公式
- 外文名:formula of a coordinates transformation
- 所屬學科:數學
- 所屬問題:高等代數(線性空間)
- 簡介:解析幾何中坐標變換公式的推廣
基本介紹


坐標變換公式的證明



























坐標變換公式(formula of a coordinates transformation)是線性空間的向量關於不同基的坐標之間的關係式,是解析幾何中(不變原點的)坐標變換公式的推廣。





























坐標變換公式(formula of a coordinates transformation)是線性空間的向量關於不同基的坐標之間的關係式,是解析幾何中(不變原點的)坐標變換公式的推廣 [1]。中文名 坐標變換公式 外文名 formula of a coordinates transformation 所屬...
這就是空間直角坐標變換公式。其中的9個係數c並不互相獨立,由於i,j,k和i′,j′,k′都是由互相正交的單位向量組成的標準正交基,方向餘弦c滿足下列6個正交條件:對應的係數矩陣(c)是正交矩陣,即(c)(c)=I.特別地,當(c)=...
在用坐標法討論變形的時候,首要的問題是選取一個適當的坐標系來化簡問題,並且常常需要把一個坐標系中的結果轉化到另一個坐標系中去。要解決這個問題,最基本的是求出同一個點在兩個不同的坐標系中的坐標變換公式。設在空間給出了...
設任一點M在坐標系x勿中的坐標為((x,婦,在坐標系x' O'夕中的坐標為(xr , yr.平面直角坐標變換公式可直接從仿射坐標變換公式導出(參見“平面仿射坐標變換”).設兩個直角坐標系都是右手系,直角標架分別是{O;t, j}和{}r; ...
已知一點對舊坐標系的坐標,從公式(2)就可以求到它對新坐標系的坐標;反之,已知一點對新坐標系的坐標,從公式(1)就可以求到它對舊坐標系的坐標。在一個方程 變換後,便得到新方程 顯然這兩個方程是表示一個相同的曲線。公...
坐標轉換是空間實體的位置描述,是從一種坐標系統變換到另一種坐標系統的過程。通過建立兩個坐標系統之間一一對應關係來實現。是各種比例尺地圖測量和編繪中建立地圖數學基礎必不可少的步驟。兩個及以上的坐標轉換時由極坐標相對參照確定維...
柱面坐標系是三大常用的坐標系之一,其它二個常用的坐標系是標準的歐氏坐標系、球坐標系。柱面坐標變換公式描述了空間中一點P在柱面坐標系下的坐標 與歐氏坐標系下的坐標 之間的變換關係。該變換關係如下述公式給出:或者,將 表達成 ...
球面坐標系是三大常用的坐標系之一,其它二個常用的坐標系是標準的歐氏坐標系、柱面坐標系。球面坐標變換公式描述了空間中一點P在歐氏坐標系下的坐標 與球面坐標系下的坐標 之間的變換關係。該變換關係如下述公式給出:或者,將表達成的...
仿射坐標變換公式(transformation formula foraffine coordinates)仿射坐標系改變時坐標的變換公式.設V是實n維線性空間,A是關於V的仿射空間,CO,E},EZ,...,En)與(Or,。 r,。 r,…,。 rO }EmEZ,...}En)是A的兩個仿射坐標系,...
19世紀末,荷蘭物理學家洛侖茲(H.A.Lorentz)在研究運動媒質中的電動力學時,提出了一套坐標變換公式,代替伽利略變換,稱為洛侖茲變換。數學形式 洛侖茲提出洛侖茲變換是基於以太存在的前提的,然而以太被證實是不存在的,相對於...
當坐標軸的方向和長度單位都不改變且只改變原點的位置時,這種坐標變換叫做“坐標軸的平移”。概念 簡稱“移軸或”平移“。公式 當把原點O(0,0)移到O'(h,k)時,則平面上任一點P的舊坐標(x,y)和他的新坐標(x',y')...
這項假設在洛倫茲變換中被捨棄,因此就算在相對論性速度下,洛倫茲變換也是成立的;而伽利略變換則是洛倫茲變換的低速近似值。以下為伽利略變換的數學表達式,其中(x,y,z,t)和(x′,y′,z′,t′)分別為同一個事件在兩個坐標系S...
點的仿射坐標變換公式 設在平面上給定了兩個仿射坐標系:{O;e,e}和{O';e',e'},分別記作σ和σ',即σ={O;e,e},σ'={O';e',e'}。設坐標系σ'的原點O'在坐標系σ下的坐標為 ,坐標系σ'的基向量e',e'...
在理論力學中,旋轉非慣性系中的物體都要受到慣性離心力和科里奧利力的作用。可以用羅德里格向量旋轉公式推導這些力的大小。設在以角速度ω,繞單位向量 k 旋轉的慣性系中,物體在 處以速度 v 運動,則物體在該局部坐標系下的運動...
平行投影也是線性變換,也可以用矩陣表示。但是透視投影不是線性變換,必須用齊次坐標表示。變換性質 編輯 用矩陣表示線性變換的一個主要動力就是可以很容易地進行組合變換以及逆變換。 [2] 組合變換:組合可以通過矩陣乘法來完成。如果A與B...
洛倫茲變換(Lorentz transformation)是狹義相對論中兩個作相對勻速運動的慣性參考系(S和S′)之間的坐標變換, [1] 是觀測者在不同慣性參考系之間對物理量進行測量時所進行的轉換關係,在數學上表現為一套方程組。洛倫茲變換因其創立者...
坐標系,是理科常用輔助方法,常見有直線坐標系,平面直角坐標系。為了說明質點的位置、運動的快慢、方向等,必須選取其坐標系。在參照系中,為確定空間一點的位置,按規定方法選取的有次序的一組數據,這就叫做“坐標”。在某一問題中...
《地圖投影與坐標變換》根據導航定位、GIS及大地測量學科的發展和套用需要,以簡明易學的方式,系統闡述了地圖投影、坐標變換的基本理論,坐標變換與轉換的方法和公式,並對常用方法給出實例。對當前我國導航定位等領域所用的等角圓柱投影、...
J.貝努利的學生J.赫爾曼在1729年不僅正式宣布了極坐標的普遍可用,而且自由地套用極坐標去研究曲線。他還給出了從直角坐標到極坐標的變換公式。確切地講,J.赫爾曼把cosθ,sinθ當作變數來使用,而且用n和m來表示cosθ和sinθ。歐拉...
曲線上任意邊線點d的坐標轉換公式為 xd=xj+ξdcosαξ-ηdsinαξ (27a)yd=yj+ξdsinαξ+ηdcosαξ (27b)已知兩點的坐標計算方位角 原計算公式為:S12=sqr( (x2-x1)2+(y2-y1)2)= sqr(△x221+△y221)A12=arcsin...
縮放變換公式為:其中,Sx、Sy、Sz是在x、y、z方向上的縮放因子。直接根據縮放公式計算得到的目標圖像中,某些映射源坐標可能不是整數,從而找不到對應的像素位置。例如,當時,圖像放大2倍,放大圖像中的像素(0, 1, 2)對應於原圖中的...
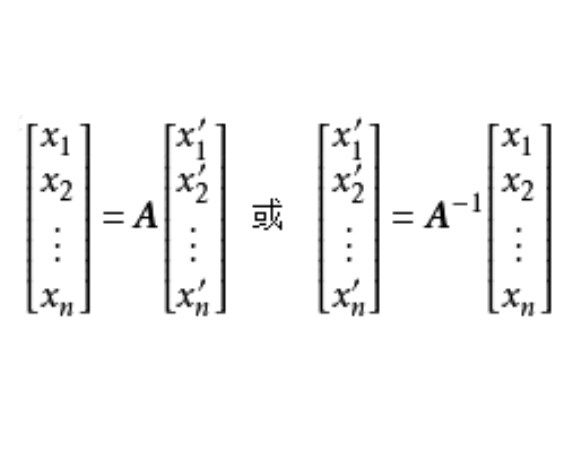
,V中一個向量在這兩組基下的坐標分別為 和 ,則 ,我們也稱 為坐標變換公式,同時也有 .例題分析 例1 設向量組 和 是R的兩個基,且有 求從基 到基 的過渡矩陣和從基 到基 的過渡矩陣。解: 由 得從基 到基 的過渡矩陣...
2.在其上執行移動操作.注意一點 : 這個坐標系的變動過程,其實是作用在"模型"的點坐標上,考慮到坐標系統3個軸向的夾角問題,需要做2次,或更多次旋轉變換來完成.公式略.,請參考 2d,3d 轉換部分.
拉普拉斯逆變換的公式是:對於所有的t>0,f(t)= mathcal ^ left =frac int_ ^ F(s)' e'ds,c' 是收斂區間的橫坐標值,是一個實常數且大於所有F(s)' 的個別點的實部值。意義與作用 為簡化計算而建立的實變數函式和復...
拉普拉斯逆變換的公式是:對於所有的t>0,;f(t)= mathcal ^ left =frac int_ ^ F(s),e^ ,ds c,是收斂區間的橫坐標值,是一個實常數且大於所有F(s),的個別點的實部值。為簡化計算而建立的實變數函式和復變數函式間的一...
派克變換(也譯作帕克變換,英語:Park's Transformation),是分析同步電動機運行最常用的一種坐標變換,由美國工程師派克(R.H.Park)在1929年提出。派克變換將定子的a,b,c三相電流投影到隨著轉子旋轉的直軸(d軸),交軸(q軸)...
相對論中的著名公式是相對論中著名公式。公示內容 公理,無法證明。2.坐標變換:由光速不變原理:dl=cdt,即dx^2+dy^2+dz^2+(icdt)^2=0在任意慣性系內都成立。定義dS為四維間隔,dS^2=dx^2+dy^2+dz^2+(icdt)^2 (1)....
載體的姿態角實際上就是載體坐標系OXYZ和地理坐標系OXYZ之間的方位關係,如圖1所示。b系相對於t系的角位置可以用一組歐拉角航向角H、俯仰角φ、橫滾角θ、來表示2個坐標系之間的變換關係,如圖2中公式。由於方向餘弦矩陣C的元素可以...
2、)兩式中的Ni稱為形函式,也叫插值函式.採用(1)式的坐標變換公式可將圖1(a)所示的不規則曲邊四邊形映射成圖1(b)所示的邊長為2的正方形單元。3、Nr是面積坐標LiLjLm的二階多項式它由節點在三角形內的位置決定與三角形單元的...
