坐標變換公式(formula of a coordinates transformation)是線性空間的向量關於不同基的坐標之間的關係式,是解析幾何中(不變原點的)坐標變換公式的推廣。
基本介紹
- 中文名:坐標變換公式
- 外文名:formula of a coordinates transformation
- 所屬學科:數學
- 所屬問題:高等代數(線性空間)
- 簡介:解析幾何中坐標變換公式的推廣
基本介紹
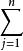

坐標變換公式的證明
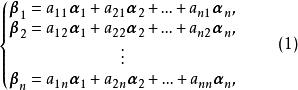
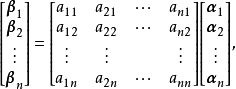
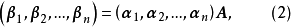

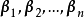
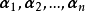
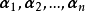
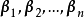
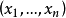



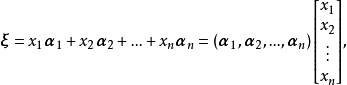
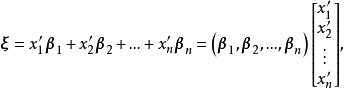



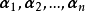
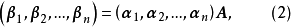
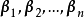
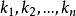
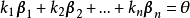

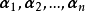
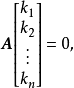
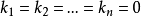
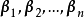
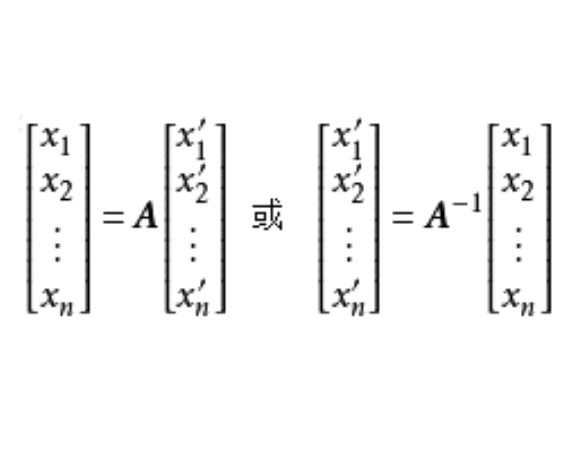
坐標變換公式(formula of a coordinates transformation)是線性空間的向量關於不同基的坐標之間的關係式,是解析幾何中(不變原點的)坐標變換公式的推廣。
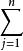

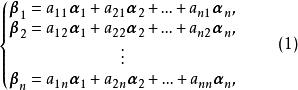
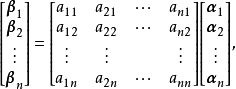
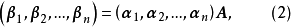

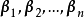
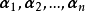
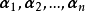
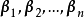
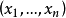



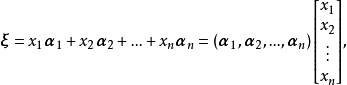
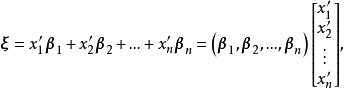



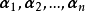
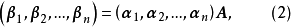
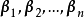
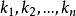
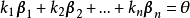

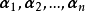
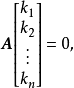
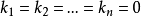
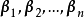
坐標變換公式(formula of a coordinates transformation)是線性空間的向量關於不同基的坐標之間的關係式,是解析幾何中(不變原點的)坐標變換公式的推廣。...
空間直角坐標變換(transformation of rectan-gular coordinates in space)是一類重要的坐標變換,空間中同一點在兩個不同的直角坐標系中的坐標之間的關係,稱為空間...
坐標轉換是空間實體的位置描述,是從一種坐標系統變換到另一種坐標系統的過程。通過建立兩個坐標系統之間一一對應關係來實現。是各種比例尺地圖測量和編繪中建立地圖...
仿射坐標變換公式(transformation formula foraffine coordinates)仿射坐標系改變時坐標的變換公式。...
基變換公式、基變換矩陣等 目錄 1 基本知識 2 相關定理 3 例題分析 基變換基本知識 編輯 在向量空間中,任一向量在指定基下的坐標是唯一的,但在不同基下的...
平移公式反映了點經過平移變換後新舊坐標之間的關係,利用平移公式可求函式解析式、平移向量的坐標、化簡函式解析式或曲線的方程等。...
球面坐標變換是指歐氏空間中一點在球面坐標系與標準歐氏坐標系之間的變換關係。...... 球面坐標變換公式描述了空間中一點P在歐氏坐標系下的坐標 與球面坐標系下的...
平面直角坐標變換(rectangular coordinates tra-nsformation in the plane)一種常用的坐標變換.指平面上任一點對於兩個直角坐標系(具有相同的長度單位)的坐標之間的...
柱面坐標變換是指歐氏空間中一點在柱面坐標系與標準歐氏坐標系之間的變換關係。...... 柱面坐標變換公式描述了空間中一點P在柱面坐標系下的坐標 與歐氏坐標系下的...
當坐標軸的方向和長度單位都不改變且只改變原點的位置時,這種坐標變換叫做“坐標軸的平移”。...
平面仿射坐標變換是一種坐標變換,指平面上任一點對於兩個仿射坐標系的坐標之間的對應關係。平面上點的仿射坐標變換公式和平面上向量的仿射坐標變換公式。...
幾何變換,又稱空間變換,是圖形處理的一個方面,是各種圖形處理算法的基礎。它將一幅圖像中的坐標位置映射到另一幅圖像中的新坐標位置,其實質是改變像素的空間位置,...
相對論中的著名公式是相對論中著名公式。中文名 相對論中的著名公式 性質 著名公式 屬性 相對論 公理,無法證明。2.坐標變換:由光速不變原理:dl=cdt,即dx^2...
R維的仿射變換與透視投影都可以用齊次坐標表示為RP維(即n+1 維的真實投影空間...縮放:縮放公式用矩陣表示為:切變:切變有兩種可能的形式,平行於x軸的切變為x...
空間直角坐標變換為站心坐標的計算公式如下[3] 站心坐標變換為空間直角坐標的計算公式如下與大地坐標系之間的轉換站心坐標系與大地坐標系之間也可以相互轉換。如果...
中心仿射變換是指含一個不變點的仿射變換,這個不變點稱為中心仿射變換的中心。在以變換中心為坐標原點的仿射坐標系中,中心仿射變換公式右端的常數項為0。例如,在...
(1)極坐標系坐標轉換為平面直角坐標系(笛卡爾坐標系)下坐標:極 坐標系中的兩個坐標 ρ和 θ可以由下面的公式轉換為直角坐標系下的坐標值:...
洛倫茲變換(Lorentz transformation)是狹義相對論中兩個作相對勻速運動的慣性參考系(S和S′)之間的坐標變換,是觀測者在不同慣性參考系之間對物理量進行測量時所...
《地圖投影與坐標變換》是2014年電子工業出版社出版的圖書,作者是王美玲、付夢印。...... 系統闡述了地圖投影、坐標變換的基本理論,坐標變換與轉換的方法和公式,並對...
拉普拉斯逆變換的公式是:對於所有的t>0,f(t)= mathcal ^ left=frac int_ ^ F(s)' e'ds,c' 是收斂區間的橫坐標值,是一個實常數且大於所有F(s)' 的...
設緩和曲線段的任意邊線點P在ZH-x′-y′坐標系中的坐標為(x′P,y′P),在j-ξ-η坐標系中的坐標為(ξP,ηP),則有坐標轉換公式〔3〕...
所謂“模型變換”,指的是從模型坐標繫到世界坐標系的轉換。3d模型在建立之初,有它自身的坐標系,以及相應的點坐標。如果把它放入一個複雜的3d模型組成的場景中的...
2.3平面向量的基本定理及坐標表示 2.4平面向量的數量積 2.5平面向量套用舉例 第三章三角恆等變換 3.1兩角和與差的正弦、餘弦和正切公式 3.2簡單的三角恆等...
