基本介紹
定義
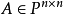

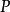
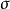
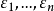

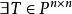
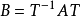
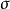
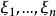
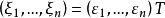
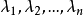
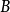

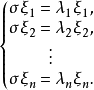
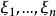
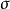
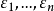
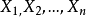


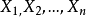
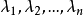
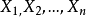
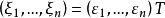
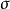
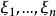
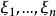
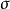
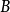
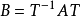
性質定理
定理1

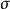

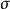



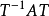

定理2
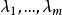
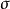
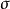
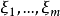
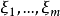
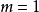
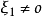
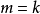
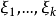
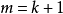
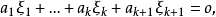
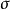
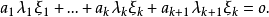
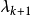
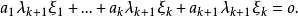
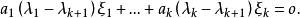
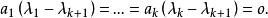
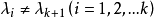
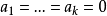
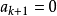
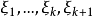

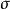
推論1
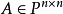

推論2


推論3
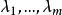
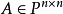
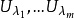
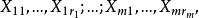
定理3
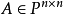
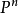

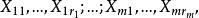
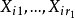
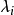
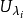
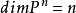
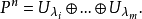
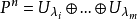


定理4
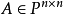
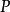
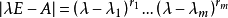
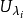
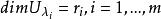

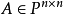

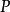
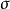
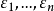

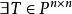
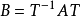
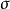
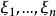
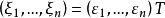
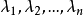
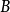

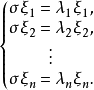
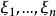
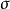
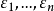
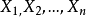


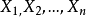
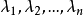
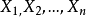
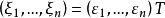
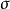
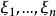
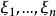
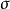
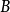
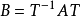

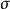

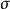



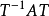

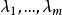
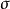
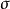
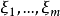
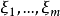
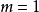
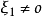
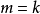
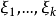
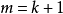
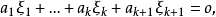
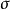
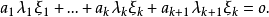
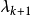
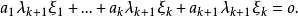
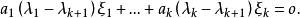
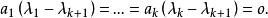
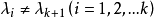
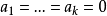
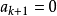
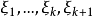

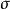
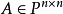



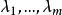
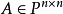
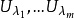
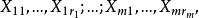
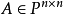
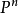

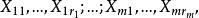
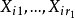
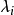
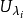
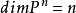
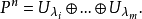
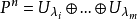


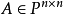
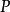
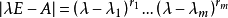
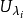
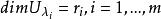
可對角化矩陣是線性代數和矩陣論中重要的一類矩陣。如果一個方塊矩陣 A 相似於對角矩陣,也就是說,如果存在一個可逆矩陣 P 使得 P −1AP 是對角矩陣,則它就...
設M為元素取自交換體K中的n階方陣,將M對角化,就是確定一個對角矩陣D及一個可逆方陣P,使M=PDP-1。設f為典範對應於M的Kn的自同態,將M對角化,就是確定Kn...
其中U和V是酉矩陣,D是對角矩陣。特徵分解是將一個矩陣A寫成PDP的形式,其中P是一個可逆矩陣,D是對角矩陣。如果A的特徵分解存在,就稱它是可對角化的矩陣。不能...
6.任意方陣C都可以用一個埃爾米特矩陣A與一個斜埃爾米特矩陣B的和表示。7.埃爾米特矩陣是正規矩陣,因此埃爾米特矩陣可被酉對角化,而且得到的對角陣的元素都是...
特點:次對角線元素不全為零,其餘元素全為零[3] 。主對角線方陣對角化 編輯 定義1 若方陣A 可以和某個對角矩陣相似,則稱矩陣A 可對角化[4] 。...
譜分解(Spectral decomposition)是將矩陣分解為由其特徵值和特徵向量表示的矩陣之積的方法。需要注意只有對可對角化矩陣才可以施以特徵分解 [17] 。...
方陣C與其共軛轉置的和是埃爾米特矩陣。任意方陣C都可以用一個埃爾米特矩陣A與一個斜埃爾米特矩陣B的和表示。埃爾米特矩陣是正規矩陣,因此埃爾米特矩陣可被酉對角化...
將上面4×4的矩陣對角化後可得本徵值:對應的本徵向量為而即為這個系統中的基態。可想而知,隨著量子系統的粒子數變多,且互動作用愈來愈複雜時,量子系統的基態...
只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。...
(8)P,Q為可逆矩陣, 則 r(PA)=r(A)=r(AQ)=r(PAQ) [4] (9)若矩陣可相似對角化則矩陣的秩等於矩陣非零特徵值的個數。...
1.實對稱矩陣A的不同特徵值對應的特徵向量是正交的。2.實對稱矩陣A的特徵值都是實數,特徵向量都是實向量。3.n階實對稱矩陣A必可相似對角化,且相似對角陣上的...
三代輕子的混合矩陣如下:其中左邊的是參與弱相互作用的中微子場,而右邊的是PMNS矩陣,還有一個由中微子場本徵態組成的矢量,將中微子質量矩陣對角化後可得這個矢量。...
第4章矩陣分解4.1矩陣的正交三角分解4.2矩陣的滿秩分解4.3矩陣的譜分解4.3.1可對角化矩陣的譜分解4.3.2正規矩陣的譜分解4.4矩陣的奇異值分解...
廣義特徵向量可以用於計算一個矩陣的若當標準型。若當塊通常不是對角化而是冪零的這個事實與特徵向量和廣義特徵向量之間的區別直接相關。...
設A為具有n個特徵值的矩陣,其中前m個特徵值相同,後n-m個不相同,我們知道後...特殊情況下即方陣A可以對角化,此時約當陣為對角陣(diagonal matrix)。...
