A為具有n個特徵值的矩陣,其中前m個特徵值相同,後n-m個不相同,則我們知道前m個特徵值對應特徵向量P1、P2......Pm,而後n-m個特徵值的特徵向量是不同的為Pm+1,Pm+2,等等。令P=[P1 P2......Pm+1 Pm+2....Pn],則J=(P-1)AP,(P-1)表示P的逆矩陣,J為約當陣(Jordan Matrix)。
基本介紹
- 中文名:約當陣
- 數學定義:為具有n個特徵值的矩陣
- 矩陣形式:圖中沒有指明數值的全為0
- 現代控制論:在現代控制理論,線性系統
非奇異變換陣,矩陣形式,現代控制論,
非奇異變換陣
設A為具有n個特徵值的矩陣,其中前m個特徵值相同,後n-m個不相同,我們知道後n-m個特徵值的特徵向量是不同的為Pm+1,Pm+2......Pn,當前m個特徵值有相同的特徵向量P1時,非奇異變換陣為P=[P1...P1 Pm+1 ...... Pn],當前m個特徵值有不同的特徵向量時,P=[P1 P2......Pm Pm+1 ...... Pn]。
矩陣形式
圖中沒有指明數值的全為0,需要指出的是前m行m列,也即m階主子矩陣為一個約當塊,J稱為約當陣。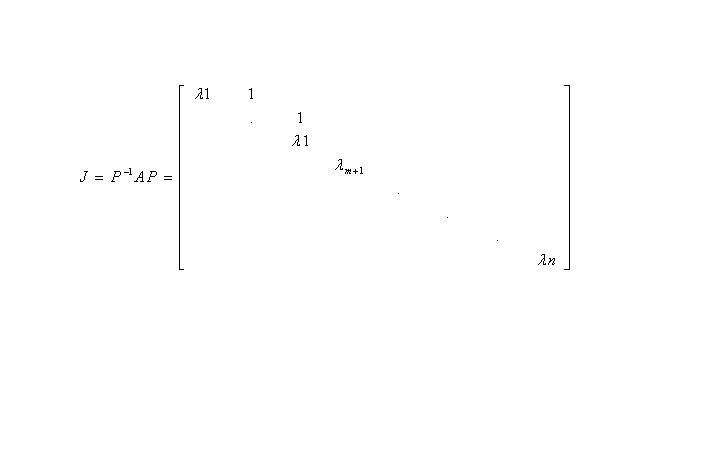

每一個方陣A(n by n)都相似一個約當陣(Jordan Matrix)。
約當陣特點是方陣A的特徵值(eigenvalues)都在對角線上,對角線上方還有若干個1。另外約當陣是由一些約當塊((Jordan Block)組成,約當塊的數量等於特徵向量(eigenvectors)的個數,這是因為每一個約當塊對應一個特徵向量。特殊情況下即方陣A可以對角化,此時約當陣為對角陣(diagonal matrix)。
現代控制論
在現代控制理論,線性系統的狀態空間分析方法中,約當陣是一種重要的規範型,屬於不能對角化的一類特殊矩陣
