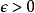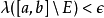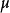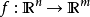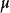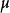相關詞條
- 盧津定理
盧津(Лузин)定理是實分析的定理。約略來說,這定理指可測函式差不多是連續函式。...
- 盧津
盧津(1883~1950)Luzin,Nikolai Nikolaevich蘇聯數學家。1883年12月9日生於托木斯克,1950年2月2日卒於莫斯科。1906年畢業於莫斯科大學,1905年和1910年曾兩次到法國...
- 葉戈羅夫定理
這個定理以俄國物理學家和幾何學家德米特里·葉戈羅夫命名,他在1911年出版了該定理。 葉戈羅夫定理與緊支撐連續函式在一起,可以用來證明可積函式的盧津定理。...
- 伯克霍夫遍歷定理
除一些涉及R中的特殊拓撲性質(如盧津定理)外,可測空間中的可測函式的性質與勒貝格可測函式的性質基本相同。例如,可測函式類對於四則運算封閉,對於極限運算封閉,...
- 李特爾伍德三原則
李特爾伍德三原則的後兩個原則分別來自盧津定理與葉戈羅夫定理,第一個原則可理解為下列結論:對於Rn中的可測集E,若m(E)<+∞,則對任意ε>0,存在有限個開區間的...
- 可測變換
除一些涉及R中的特殊拓撲性質(如盧津定理)外,可測空間中的可測函式的性質與勒貝格可測函式的性質基本相同。例如,可測函式類對於四則運算封閉,對於極限運算封閉,...
- 奧爾利奇空間
除一些涉及R中的特殊拓撲性質(如盧津定理)外,可測空間中的可測函式的性質與勒貝格可測函式的性質基本相同。例如,可測函式類對於四則運算封閉,對於極限運算封閉,...
- 強可測矢量值函式
對於強可測函式而言,也有相應的葉戈羅夫定理和盧津定理。葉戈羅夫定理斷言:如果(Ω,𝓕,μ)有限測度空間,而定義在Ω上取值於巴拿赫空間X的強可測向量值函式列{xn...
- 實分析引論
附錄4.2盧津生平第5章積分§5.1非負簡單函式的積分§5.2非負可測函式的積分§5.3一般可測函式的積分§5.4積空間§5.5傅比尼定理...
- 強可測向量值函式
此外,對於強可測函式而言,也有相應的葉戈羅夫定理和盧津定理‘葉戈羅夫定理斷言:如果(月,夕一,川是有限測度空間,而定義在刀上取值於巴拿赫空間X的強可測向量值函式...