基本介紹
歷史發展
泰勒簡介
發展過程
公式形式
泰勒公式形式

 泰勒公式
泰勒公式餘項
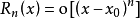




帶佩亞諾餘項






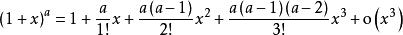
驗證推導
公式推導

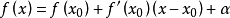

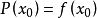



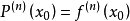
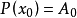

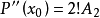








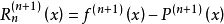





麥克勞林展開



 近似表達正弦函式
近似表達正弦函式公式套用

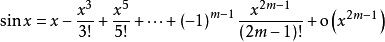








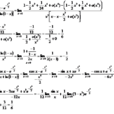
泰勒定理一般指本詞條

 泰勒公式
泰勒公式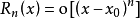










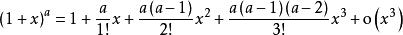

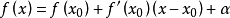

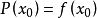



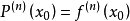
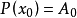

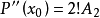








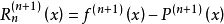








 近似表達正弦函式
近似表達正弦函式
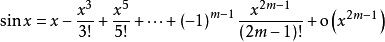








數學中,泰勒公式是一個用函式在某點的信息描述其附近取值的公式。如果函式足夠平滑的話,在已知函式在某一點的各階導數值的情況之下,泰勒公式可以用這些導數值做...
布魯克·泰勒(英語:Brook Taylor,1685年8月18日-1731年11月30日)出生於英格蘭密德薩斯埃德蒙頓,逝世於倫敦,是一名英國數學家,他主要以泰勒公式和泰勒級數出名。...
在數學中,泰勒級數(英語:Taylor series)用無限項連加式——級數來表示一個函式,這些相加的項由函式在某一點的導數求得。泰勒級數是以於1715年發表了泰勒公式的...
泰勒法則,即標準泰勒(Taylor)規則是常用的簡單貨幣政策規則之一,由泰勒於1993年針對美國的實際數據提出。泰勒規則描述了短期利率如何針對通脹率和產出變化調整的準則...
標準泰勒規則(Taylor rule)是常用的簡單貨幣政策規則之一,由史丹福大學的約翰.泰勒於1993年根據美國貨幣政策的實際經驗,而確定的一種短期利率調整的規則。...
泰勒士 國籍 古希臘 民族 希臘人 出生地 米利都 出生日期 約公元前624...在數學上,泰勒斯定理以他的名字命名,其內容為:若A,B,C是圓周上的三點,且AC...
康托爾-伯恩斯坦-施洛德定理(伯恩斯坦定理)(Cantor-Bernstein-Schroeder theorem)是集合論中的一個基本定理,得名於康托爾、Felix Bernstein 和 Ernst Schröder。該...
弗雷歇-泰勒公式(Frechet-Taylor formula)是經典的泰勒公式在F微分意義下的推廣。...... (x)在x0處的泰勒展開式,剩餘的Rn(x)是泰勒公式的餘項,是(x-x0)n的...
費馬大定理,又被稱為“費馬最後的定理”,由17世紀法國數學家皮耶·德·費瑪提出。他斷言當整數n >2時,關於x, y, z的方程 x^n + y^n = z^n 沒有正...
中值定理是反映函式與導數之間聯繫的重要定理,也是微積分學的理論基礎,在許多方面它都有重要的作用,在進行一些公式推導與定理證明中都有很多套用。中值定理是由眾多...
微分中值定理主要包括羅爾定理、拉格朗日定理、柯西定理、泰勒定理,其中羅爾定理是拉格朗日定理等的預備定理,由三個已知條件推得結果,三個已知條件缺一不可,即若要...
四色定理(世界近代三大數學難題之一),又稱四色猜想、四色問題,是世界三大數學猜想之一。四色定理的本質正是二維平面的固有屬性,即平面內不可出現交叉而沒有公共點...
棣莫弗定理由法國數學家棣莫弗(1667-1754年)創立。指的是設兩個複數(用三角函式形式表示)Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),則:Z1Z2=...
蝴蝶定理(Butterfly Theorem),是古代歐氏平面幾何中最精彩的結果之一。這個命題最早出現在1815年,由W.G.霍納提出證明。而“蝴蝶定理”這個名稱最早出現在《美國數學...
牛頓-萊布尼茲公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函式的原函式或者不定積分之間的聯繫。牛頓-萊布尼茨公式的內容是一個...
麥克勞林公式是泰勒公式的一種特殊形式。...... 麥克勞林公式是泰勒公式的一種特殊形式。中文名 麥克勞林...他得到數學分析中著名的Maclaurin級數展開式,並用待定係數...
在工程實際問題的最佳化設計中,所列的目標函式往往很複雜,為了使問題簡化,常常將目標函式在某點鄰域展開成泰勒多項式來逼近原函式,此時函式在某點泰勒展開式的矩陣形式...
