正切值是指是直角三角形中,某一銳角的對邊與另一相鄰直角邊的比值。對於任意一個實數x,都對應著唯一的角,而這個角又對應著唯一確定的正切值tanx與它對應,按照這個對應法則建立的函式稱為正切函式。
基本介紹
- 中文名:正切值
- 外文名:tan
- 定義:銳角的對邊與相鄰直角邊的比值
- 類型:三角函式
數學概念
概述
 正切值的單位圓表示及正切函式圖像
正切值的單位圓表示及正切函式圖像 tanα=b/a
tanα=b/a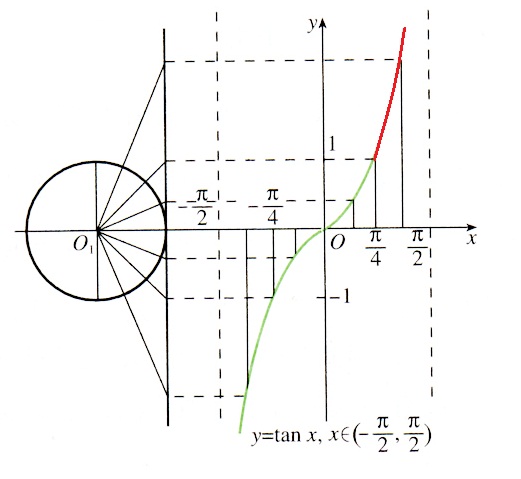
正切值是指是直角三角形中,某一銳角的對邊與另一相鄰直角邊的比值。對於任意一個實數x,都對應著唯一的角,而這個角又對應著唯一確定的正切值tanx與它對應,按照這個對應法則建立的函式稱為正切函式。
 正切值的單位圓表示及正切函式圖像
正切值的單位圓表示及正切函式圖像 tanα=b/a
tanα=b/a正切值是指是直角三角形中,某一銳角的對邊與另一相鄰直角邊的比值。對於任意一個實數x,都對應著唯一的角,而這個角又對應著唯一確定的正切值tanx與它對應,按照...
Tan是正切的意思,角θ在任意直角三角形中,與θ相對應的對邊與鄰邊的比值叫做角θ的正切值。若將θ放在直角坐標系中即tanθ=y/x。tanA=對邊/鄰邊。在直角...
餘弦相似度,又稱為餘弦相似性,是通過計算兩個向量的夾角餘弦值來評估他們的相似度。餘弦相似度將向量根據坐標值,繪製到向量空間中,如最常見的二維空間。...
圓.做過圓和x軸交點的切線.則,從原點引出的一條射線,與這條切線的交點,到x軸的垂線,就是射線與x軸正向之間的角度的正切線.它的長度就等於這個角的正切值....
正弦值是在直角三角形中,對邊的長比上斜邊的長的值。 任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值。...
atan可返回數字的反正切值。...... atan可返回數字的反正切值。中文名 可返回數字的反正切值 外文名 atan 功能 : 反正切函式(C++) 用法: double atan(dou...
半角公式(Half angle formula)是利用某個角(如∠A)的正弦值、餘弦值、正切值,及其他三角函式值,來求其半角的正弦值,餘弦值,正切值,及其他三角函式值的公式。....
6、高壓介質損耗測量儀 簡稱介損儀,是指採用電橋原理,套用數字測量技術,對介質損耗角正切值和電容量進行自動測量的一種新型儀器。一般包含高壓電橋、高壓試驗電源和...
銳角三角函式是以銳角為自變數,以比值為函式值的函式。我們把銳角∠A的正弦、餘弦、正切和餘切都叫做∠A的銳角函式。...
正切值在 隨角度增大(減小)而增大(減小);餘切值在 隨角度增大(減小)而減小(增大);正割值在 隨著角度的增大(或減小)而增大(或減小);...
介紹atan( ) 函式 返回數值表達式的反正切弧度值。語法ATAN(nExpression)參數nExpression 指定一個數值表達式,atan( ) 函式返回此數值表達式的反正切值。nExpression...
反三角函式是一種基本初等函式。它是反正弦arcsin x,反餘弦arccos x,反正切arctan x,反餘切arccot x,反正割arcsec x,反餘割arccsc x這些函式的統稱,各自表示...
斜率,亦稱“角係數”,表示一條直線相對於橫軸的傾斜程度。一條直線與某平面直角坐標系橫軸正半軸方向的夾角的正切值即該直線相對於該坐標系的斜率。 如果直線與x...
正切值在 隨角度增大(減小)而增大(減小);餘切值在 隨角度增大(減小)而減小(增大);正割值在 隨著角度的增大(或減小)而增大(或減小);...
arccos表示的是反三角函式中的反餘弦。一般用於表示當角度為非特殊角時。由於是多值函式,往往取它的單值,值域為[0,π],記作y=arccosx,我們稱它叫做反三角函式...
表示一條直線(或曲線的切線)關於(橫)坐標軸傾斜程度的量。它通常用直線(或曲線的切線)與(橫)坐標軸夾角的正切,或兩點的縱坐標之差與橫坐標之差的比來表示。...
坡比,即坡面的垂直高度h和水平寬度l的比,即坡角的正切值 (tan∠a值∠a為斜坡與水平面夾角)。「亦即tan∠α」。通常用“i”表示。角a的正切=垂直距離/水平...
若要用度表示反正切值,請將結果再乘以 180/3.14159。另外要注意的是,函式atan2(y,x)中參數的順序是倒置的,atan2(y,x)計算的值相當於點(x,y)的角度值。...
