柯西-施瓦茨不等式

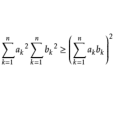
柯西不等式，是數學家柯西(Cauchy)在研究數學分析中的“流數”問題時得到的。

從歷史的角度講，柯西不等式應稱作Cauchy-Buniakowsky-Schwarz不等式（柯西-布尼亞科夫斯基-施瓦茨不等式），因為正是後兩位數學家彼此獨立地在積分學中推而廣之，才將這一不等式套用到近乎完善的地步。

基本介紹

• 中文名：柯西不等式
• 外文名：Cauchy-Buniakowsky-Schwarz Inequality
• 提出者：奧古斯丁·路易·柯西
• 提出時間：18世紀
• 推廣者：赫爾曼·阿曼杜斯·施瓦茨
• 套用學科：數學

柯西簡介

柯西（Cauchy Augustin-Louis，1789－1857），法國數學家，1789年8月21日生於巴黎，他的父親路易·弗朗索瓦·柯西是法國波旁王朝的官員，在法國動盪的政治漩渦中一直擔任公職。由於家庭的原因，柯西本人屬於擁護波旁王朝的正統派，是一位虔誠的天主教徒。

他在純數學和套用數學的功底是相當深厚的，很多數學的定理、公式都以他的名字來稱呼，如柯西不等式、柯西積分公式。在數學寫作上，他被認為在數量上僅次於歐拉的人，他一生一共著作了789篇論文和幾本書，以《分析教程》（1821年）和《關於定積分理論的報告》（1827年）最為著名。不過他並不是所有的創作都質量很高，因此他還曾被人批評“高產而輕率”，這點倒是與數學王子（高斯）相反。據說，法國科學院《會刊》創刊的時候，由於柯西的作品實在太多，以致於科學院要負擔很大的印刷費用，超出科學院的預算，因此，科學院後來規定論文最長的只能夠到四頁。柯西較長的論文因而只得投稿到其它地方。

定義定理

二維形式

公式變形：

等號成立條件：若且唯若（即）時。

一般形式

等號成立條件：，或中有至少一方全為零。

上述不等式等同於概述圖中的不等式。

一般形式推廣

此推廣形式又稱卡爾松不等式，其表述是：在m×n矩陣中，各列元素之和的幾何平均不小於各行元素的幾何平均之和。二維形式是卡爾松不等式n=2時的特殊情況。

向量形式

推廣：

三角形式

等號成立條件：，且ac+bd0（即）。

機率論形式

積分形式

一般形式

設V是一線性空間，在V上定義了一個二元實函式，稱為內積，記做，它具有以下性質：

1、

2、

3、

4、，若且唯若時(α，α)=0

並定義 α 的長度，則柯西不等式表述為：

驗證推導

二維形式的證明

等號在且僅在ad－bc=0即ad=bc時成立。

三角形式的證明

兩邊開平方得：

向量形式的證明

（只是對二維的說明）

機率論形式的證明

機率論形式的證明

積分形式的證明

構造一個二次函式，

所以該二次函式與x軸至多一個交點， ，

即

若且唯若 與 線性相關時 等號成立。

一般形式的證明

剩餘幾種情形都是一般情形的特例，完全可以用一般情形的證明方法來證。

另一種寫法：

定理推廣

複變函數中

若函式在區域D及其邊界上解析，為D內一點，以為圓心做圓周，只要及其內部G均被D包含，則有：

其中M是的最大值， 。

證明：有柯西積分公式可知

所以

利用柯西-比內公式還可得到更廣義的柯西不等式如下:令A,B為兩個m×n矩陣(m＞n),則有:det(A*AT)*det(B*BT)≥(det(A*BT))^2

其他不等式

其他不等式敬請參見以下詞條：

卡爾松不等式

琴生不等式

均值不等式

絕對值不等式

權方和不等式

赫爾德不等式

閔可夫斯基不等式

伯努利不等式

排序不等式

基本不等式

套用例子

柯西不等式在求某些函式最值中和證明某些不等式時是經常使用的理論根據，技巧以拆常數，湊常值為主。

巧拆常數證不等式

例：設a、b、c為正數且互不相等，求證：。

證明：將a+b+c移到不等式的左邊，化成：

=

由於a、b、c為正數且互不相等，等號取不到。

附用基本不等式證 設 ，則所證不等式等價於

。

因為。 所以上式顯然成立。

求某些函式最值

例：求函式的最大值。

函式的定義域為[5，9]，y＞0，由柯西不等式變形

則。

函式僅在，即時取到。