朗道量子化是指均勻磁場中帶電粒子的迴旋軌道發生的量子化。這些帶電粒子能量在一系列分立的數值中取值,形成朗道能級。朗道能級是簡併的,每一能級上電子的電子數量與外加磁場的強度成正比。由朗道量子化可以得出外磁場會導致材料中電子性質的振盪。這一理論是由蘇聯物理學家列夫·朗道於1930年提出的。
基本介紹
- 中文名:朗道量子化
- 外文名:landau quantization
- 提出者:列夫·朗道
- 提出時間:1930年
- 學科:量子力學
- 相關術語:朗道能級
推導







朗道能級




討論
規範變換影響



















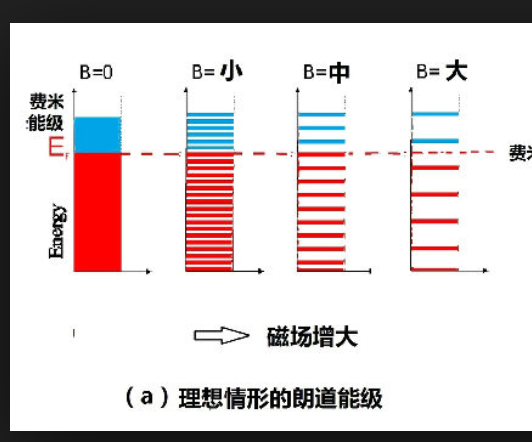
朗道量子化是指均勻磁場中帶電粒子的迴旋軌道發生的量子化。這些帶電粒子能量在一系列分立的數值中取值,形成朗道能級。朗道能級是簡併的,每一能級上電子的電子數量與外加磁場的強度成正比。由朗道量子化可以得出外磁場會導致材料中電子性質的振盪。這一理論是由蘇聯物理學家列夫·朗道於1930年提出的。






























朗道量子化是指均勻磁場中帶電粒子的迴旋軌道發生的量子化。這些帶電粒子能量在一系列分立的數值中取值,形成朗道能級。朗道能級是簡併的,每一能級上電子的電子數量與外加磁場的強度成正比。由朗道量子化可以得出外磁場會導致材料中電子...
列夫·達維多維奇·朗道的研究工作涵蓋了從流體力學到量子場論的各個理論物理學分支。人物生平 1908年1月22日,列夫·達維多維奇·朗道出生於俄羅斯帝國巴庫(現亞塞拜然)的一個知識分子家庭。1912年,4歲能閱讀書籍,7歲學完中學數學課程...
1932—1937年,朗道在哈爾科夫擔任烏克蘭物理技術研究所理論部主任。從1937年起在莫斯科擔任蘇聯科學院物理問題研究所理論部主任。目錄 第一章 量子力學的基本概念.1 不確定性原理 2 疊加原理 3 算符 4 算符的加法和乘法 5 連續譜 6 ...
由金茲堡和朗道建立的超導電性巨觀理論。該理論綜合了超導體的電動力學、量子力學和熱力學性質。 金茲堡-朗道理論(GLTheory)是一種重要的唯象超導理論(1950)。與London方程及Pippard非局域理論相比較,GL理論獨到之處是可以處理強磁場和...
在凝聚態物理學中,量子振盪描述了一系列相關的實驗技術,用於在存在強磁場的情況下映射金屬的費米面。這些技術基於費米子在磁場中運動的朗道量子化原理。對於強磁場中的自由費米子氣體,能級被量化成帶,稱為朗道能級,其分離度與磁場...
25800歐姆。2013年3月15日,這個成果線上發表在《科學》雜誌上。這一發現可被用於發展新一代低能耗電晶體和電子學器件,進而推動信息技術的進步。參見 石墨烯 霍爾效應 霍爾效應感測器 朗道量子化 ...
一些理論經典的對稱性在量子理論中不再成立—這個現象稱為一個反常。最出名的包括:共形反常,它導致了一個變動耦合常數。在QED中,這導致了朗道奇點(Landau pole)。在量子色動力學(QCD)中,這導致漸近自由。手征反常,出現在費米子...
德哈斯-范阿爾芬效應(英文: De Haas-van Alphen effect)是指純金屬晶體的磁化強度隨外加磁場的增加而發生振盪的現象。它是一種量子力學效應。產生這種效應的物理原因是由於金屬晶體的電子能態的“朗道量子化”引起的。此時金屬的電子在...
這是首次在凝聚態材料體系里觀察到non-Abelian規範勢,這一發現也預示著可以通過轉角很好的調製石墨烯的電學性質;我們系統測量了不同轉角雙層石墨烯的朗道量子化,深入研究了其費米速度隨轉角以及耦合強度的關係,證明轉角和耦合強度都可以...
通過輸運手段測量贗磁場作用下的朗道量子化現象對石墨烯在電子器件的套用意義重大。本項目基於應變工程的最新進展,在石墨烯中通過襯底的變化獲得不同應變的褶皺結構,建立褶皺結構表面曲率與產生贗磁場大小之間的關係,為褶皺結構調控贗磁場的...
磁場下,電子的運動將會量子化而形成朗道能級,如體系是三維的,則朗道能級在沿著磁場方向是有色散的。研究發現,在第二類外爾半金屬中,能量傾斜會使得體系的朗道能級間距變小,特別是當磁場指向偏移能量傾斜方向為某個臨界角度時,朗道...
通過在拉伸時測量納米線的電導率,科學家發現:當納米線長度縮短時,它的電導率也以階梯的形式隨之縮短,每階之間相差一個朗道常數G。因為低電子濃度和低等效質量,這種電導率的量子化在半導體中比在金屬中更加明顯。量子化的電導率可以...
