簡介 如圖1所示,眾所周知,材料體系按照其電子能帶結構的不同可以劃分為
金屬 和
絕緣體 。近年來的研究表明,絕緣體可以進一步細分為平庸絕緣體和
拓撲絕緣體 。拓撲絕緣體表現出與一般絕緣體完全不一樣的量子現象與物性,例如:拓撲保護的表面態、反弱局域化、量子自旋、
反常霍爾效應 等等。因此從被發現後,拓撲絕緣體立即成為了
凝聚態物理 、
材料科學 中的一大熱點研究領域。
圖1 拓撲絕緣體 的一個重要特性是,小的微擾對其拓撲不會有影響,這就使得人們可以定義絕緣體的拓撲性質(也就是說,只要這個微擾不關閉絕緣體的
能隙 ,絕緣體的拓撲性質就不會發生改變)。近年來人們發現了一類特別的金屬體系,它們的低能激發可以用粒子物理中的 2 分量狄拉克(Dirac)方程即外爾(Weyl)方程來描述,因此這類材料體系被稱為Weyl 半金屬。Weyl 半金屬雖然沒有能隙,但是仍然具有拓撲非平庸行為。
外爾半金屬是一種新穎的
量子態 ,其電子的色散關係存在著成對的手性相反的外爾點,這對外爾點可以看成是倒空間中一對正負磁荷(magnetic monopole)。這對磁荷在磁場的作用下發生類似於Zeeman效應的能級劈裂,從而導致不同手性的電子密度的不同。因此,當外加電場與磁場平行時,倒空間中不同手性間的散射由於正負手性Weyl點間的距離增加而導致相應的谷間散射(intervalley scattering)減弱,從而產生了負磁阻效應,既所謂手性反常。如圖2所示是在磁場作用下一對手性相反的狄拉克錐在倒空間被拉開的示意圖。該效應最早由Adler, Bell和Jackiw在粒子物理中提出(簡稱為ABJ效應)。最近,該效應在凝聚態物理中的外爾半金屬也被觀察到。
圖2.在磁場作用下一對手性相反的狄拉克錐在倒空間被拉開的示意圖 分類 第一類外爾半金屬 1929 年,物理學家Hermann Weyl 理論預言了一種質量為零的相對論性費米子,稱為“
外爾費米子 ”。獨特的是,這種費米子具有兩種不同的類型,可以用“手征”來表示,其中一種費米子的自旋和動量方向平行,而另一種費米子相反,稱它們分別具有“右手”和“左手”手征,如同人的左手和右手一樣,具有鏡像對稱性。通常人們研究的費米子“右手”和“左手”手征分量是無法分離的,因此如果在實驗上能夠實現兩種外爾費米子的分離,將可能觀測到新的物理現象,也將為探索“手征電子學”和發展下一代低功耗信息器件提供新的契機。
最初人們一直在高能物理中尋找外爾費米子,中微子曾經被認為是外爾費米子,但後來發現中微子有質量,尋找外爾費米子的道路變得更加坎坷。理論預言近80年後,凝聚態物理中拓撲能帶理論的發展給人們帶來了新的希望。在固體材料中,電子的運動會受到晶格周期勢場的影響,同時受到其他電子的相互作用。而在某些特殊晶格中,電子的集體行為可以用一種新的“準粒子”來描述。隨後的研究發現,在一些破壞空間或時間反演對稱性的固體材料中,如果能帶中導帶和價帶相交於一點,那么在交點處滿足線性色散關係的低能準粒子可以等效地對應於高能物理中的無質量外爾費米子。2011 年,南京大學萬賢剛教授首次預言了第一種存在外爾費米子的固體材料Y
2 Ir
2 O
7 ,該材料具有磁性,但由於磁性會影響實驗上對外爾點的觀測,不容易證實外爾費米子的存在。2015年,
中國科學院物理研究所 以及Princeton大學的物理學家們終於在破壞空間反演對稱性的固體材料TaAs 中發現了外爾費米子,具有外爾費米子的固體材料稱為外爾半金屬。自此,越來越多的理論和實驗工作迅速開展起來。以TaAs 為代表的外爾半金屬中,外爾點附近的能帶是直立的“X”型錐體(圖3),費米子滿足洛倫茲對稱性,稱為“第一類外爾費米子”。
圖3.兩種類型的外爾點周圍能帶 圓錐的頂點(稱為Weyl點)就代表
Weyl費米子 。不同手性的Weyl費米子只能同時產生或者消失。在這個點的附近,材料體內作為準粒子的電子具有與無質量Weyl費米子相同的運動特性。Weyl點的另一個意義是,它其實是動量空間的“時空奇點”。我們可以把它形象地類比於時空隧道,就像物理中所描述的蟲洞。這些特殊的奇點對材料表面上電子有很強的影響,比如當表面電子沿某些特定方向運動並達到特定速度時,會突然從表面消失,進入材料體內,並立刻從材料的另一個表面穿出,就像是一艘經歷了“蟲洞”旅行的宇宙飛船。更進一步,不同手性的Weyl點會在表面的電子態中形成一些非閉合的曲線,使Weyl點彼此互相連線,這就是費米弧。由於這類半金屬是受到拓撲保護的,所以這個費米弧也叫拓撲費米弧。不僅如此,Weyl半金屬還有另一個令人興奮的性質:負磁阻效應。當外加平行的電場和磁場時,動量空間中左旋的Weyl點和右旋Weyl點會分離開,而Weyl費米子可以從右旋的Weyl點出發被發射到左旋的Weyl點去,就好比金屬中的電子產生定向運動時會有電流。隨著磁場的增加,越來越多的Weyl費米子參與到輸運中,使得材料的電阻降低。磁場在這裡猶如水泵般將電子“泵”出來,實際中產生的效應就是“負磁阻”效應。
第二類外爾半金屬 第二類外爾半金屬是外爾半金屬概念的推廣,其特徵是在外爾點附近的狄拉克錐是傾斜的,因此相應的電子色散關係在外爾點附近不滿足洛倫茨變換對稱性。理論上預言第二類外爾半金屬有二個實驗特徵:(1)外爾點附近傾斜的電子色散關係;(2) 各向異性的負磁阻,即在ab-面僅有一個方向上存在由於ABJ-效應導致的負磁阻。WTe2 是第一個理論預言的第二類外爾半金屬材料。
由於WTe
2 的外爾點高於費米能級60 meV,因此需要通過一定方法提高費米能才能在輸運實驗中觀測到ABJ效應。研究組精確控制晶體生長和退火工藝,研製成功WTe
1.98 晶體並發現了各向異性ABJ-效應:在a-和b-方向均發現了ABJ-效應。圖4是WTe
1.98 晶體沿著a-和b-方向的磁阻隨溫度、磁場與電場間的夾角間的實驗關係。詳細的數據擬合證明沿著b-方向的ABJ-效應係數比沿著a-方向的大70%。這個實驗結果看似與理論預言的二類外爾半金屬特徵(2)不吻合,但輸運理論分析表明該預言僅適用於理想量子條件,而在經典近似條件下,第二類外爾半金屬的ABJ效應仍然是各向同性的。我們的實驗結果則正好位於極端量子情況和經典近似情況之間,即處於準經典區域,因此作為一個自然的過渡,我們在a-和b-方向都觀察到了ABJ效應,但是b-方向的ABJ效應較強。
圖4.ABJ效應導致的負磁阻強烈依賴於溫度以及磁場和電場間的夾角 實驗還發現:溫度大於30K時ABJ效應就消失了。其可能的原因是溫度導致的拓撲轉變。為了證明這個推測,又測量了從20 K到300 K的WTe2 晶體的晶格常數變化。利用第一性原理計算證明:外爾點僅在60 K以下才出現,而在60 K以上外爾點處出現了一個非常小的能隙。這充分說明WTe2 第二類外爾半金屬態對晶格常數/溫度異常敏感。
這個工作證明:第二類外爾半金屬在準經典條件下會出現各向異性的ABJ效應;對於WTe2 材料,其二類外爾半金屬態對於溫度/晶格常數非常敏感。這些結果展示了第二類外爾半金屬材料豐富的物理特性,深化了對第二類外爾半金屬材料這一類新的拓撲材料物理的認識。
外爾方程 外爾
(Weyl) 方程在
Dirac 方程被提出一年以後,
Weyl 發現,當
Dirac 方程中的質量為零時,該方程可以變成 Weyl 方程:
iℏ ∂/∂ t ·Ψ = H·Ψ , H = cσ · p
Weyl 方程是靜止質量為零、自旋為 1/2 的粒子 滿 足 的 兩 分 量 波 動 方 程 。 Weyl 方 程 中 有[ σ · p , H ] = 0 ,所以 σ · p σ · p / | p | 是自旋沿動量方向的投影,也是守恆量。為 ( σ · p ) /| p | *( σ · p ) /| p |= 1 ,所以有 ( σ · p ) /| p | = ±1 ,其中取+1 的為右旋粒子態,取-1的為左旋粒子態。1930年Pauli 認為在β 衰變過程中,除了電子之外,同時還產生靜止質量為零而且電中性的中微子。很自然,人們認為中微子是一種 Weyl 費米子,它的行為可以用 Weyl 方程描寫。但是後來人們發現中微子是有質量的粒子。在人們已知的粒子中,沒有一個屬於 Wey l費米子。有意思的是,最近人們預言有些凝聚態體系的低能激發可以用 Weyl 方程來描述,這類材料被命名為 Weyl 半金屬。
研究現狀 (1) 北京大學量子材料科學中心 博士生蔣慶東在導師謝心澄教授指導下,與中心孫慶豐教授、劉海文助理研究員,以及
蘇州大學 江華教授合作,在外爾半金屬研究領域取得重要進展,文章以
Topological Imbert-Fedorov Shift in Weyl Semimetals 為題線上發表於《物理評論快報》
( Physics Review Letters 115,156602) 。
外爾半金屬由於其理論和實驗方面的重大進展受到
凝聚態 和材料領域的廣泛關注。最近,科學家在TaAs族化合物中證實了
外爾費米子 的存在。外爾費米子靜質量為零且具有特定的手性,從而可能具有奇特的物理特性。 蔣慶東等人注意到:儘管統計規律不同,外爾費米子和光子有許多相似特性(例如: 都具有無質量、
手性 等特點)。因此,外爾
半金屬 體系中將存在特定的類光學效應。他們的工作主要研究外爾半金屬中的
Goos-H"a" ̈nchen 位移 和
Imbert-Fedorov 位移 。
光學中
Goos-H"a" ̈nchen 位移和
Imbert-Fedoro 位移是指光在界面反射過程中可能會存在的縱向偏移和橫向偏移。蔣慶東等人的研究表明,外爾費米子在界面反射過程中也存在縱向偏移和橫向偏移(圖6)。他們進一步發現橫向位移
(Imbert-Fedorov 位移) 不僅具有手性依賴(谷依賴)的特點,而且起源於體系的拓撲性質,即外爾半金屬獨特的貝里曲率。基於
Imbert-Fedorov 位移具有手性依賴的特點,多次界面反射後不同手性的外爾費米子能被空間分離(圖7)。這一性質可被利用於:(1)有效表征某個體系是否為外爾半金屬;(2)製備谷電子學器件;(3)通過測定
Imbert-Fedorov 位移得到體系的貝里曲率。正如審稿人評論說:這項理論研究工作解決了該領域兩個較為重要的課題: 如何有效表征外爾半金屬和如何測量貝里曲率。
圖6 圖7 (2) 北京理工大學 物理學院量子功能材料設計與套用實驗室姚裕貴教授研究組(余智明博士後、姚裕貴教授)和
新加坡科技設計大學 的楊聲遠教授合作研究了第二類外爾半金屬在磁場下的新奇物性。相關研究成果發表在近期的《物理評論快報》上[Phys. Rev. Lett.117, 077202 (2016)]。該工作得到了國家自然科學基金委和科技部的資助。
在實驗室中模擬和研究基本粒子(如
狄拉克費米子 、
外爾費米子 )的行為是當前凝聚態物理中最為令人振奮的研究領域之一。更為吸引人的是,由於電子在凝聚態物理領域中和基本粒子在高能物理領域中所遵循的物理規範可有所不同,所以
凝聚態物理 中還能呈現出高能物理中所不存在的有效
費米子 ,如最近提出的第二類外爾(狄拉克)費米子等諸多新型費米子。一般而言,動量空間中外爾費米子的
色散 是可以沿某一動量方向傾斜的。當傾斜足夠強的時候,外爾錐將會翻倒而使得體系的費米面從一個點變為一條線或一個面。此種情況下的外爾費米子被稱為第二類外爾費米子,以區分於傳統的第一類外爾費米子。儘管外爾費米子的手性並不受能帶傾斜的影響,但在凝聚態物理中諸多物理行為都與體系費米面的幾何形貌息息相關,所以第二類外爾費米子具有迥異於傳統外爾費米子和其它材料的新奇物性。
磁場下,電子的運動將會量子化而形成
朗道能級 ,如體系是三維的,則朗道能級在沿著磁場方向是有色散的。研究發現,在第二類外爾半金屬中,能量傾斜會使得體系的朗道能級間距變小,特別是當磁場指向偏移能量傾斜方向為某個臨界角度時,朗道能級的間距為零,也即導致所謂的朗道能級坍塌現象
(collapse of Landau levels) 基於半經典的物理圖像,他們還指出了此坍塌現象對應於電子在磁場中的迴旋運動軌道由閉合變為開放,表明此時有效外爾模型已不足以描述電子的行為。在朗道能級坍塌之前,第二類外爾點的朗道能級的磁光電導亦表現出與傳統外爾材料的迥異行為:如具有各向異性的磁光電導,低頻下一直存在帶間躍遷,且隨頻率增加,光學吸收譜具有獨特的形狀等。這些發現皆有助於指導實驗發現第二類外爾費米子材料和確定體系參數。
圖8 圖8:(a)朗道能級壓縮因子隨能量傾斜與磁場夾角的變化行為。(上):傳統外爾點,(下):第二類外爾點,其中紅線表示出現朗道能級坍塌的臨界角。(b)磁場下電子的半經典軌道隨磁場方向變化的演化行為。軌道由封閉變為開放對應於體系從具有良好定義的朗道能級到朗道能級的坍塌(外爾模型下的描述)。
圖9 圖9:(a)第二類外爾點和(c)傳統外爾點在能量傾斜方向與磁場平行的情況下的朗道能級。(b)和(d)與(a)和(c)類似,但此時能量傾斜方向與磁場反平行。(e)外爾點的縱向磁光電導,其中紅線對應於(a)中的第二類外爾點,藍線對應於(c)中的傳統外爾點。(f)與(e)類似,但分別對應的是(b)和(d)中外爾點的行為。
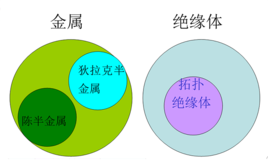 圖1
圖1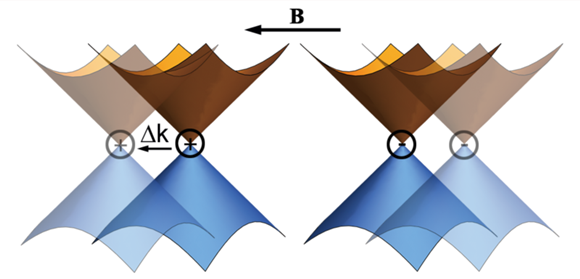 圖2.在磁場作用下一對手性相反的狄拉克錐在倒空間被拉開的示意圖
圖2.在磁場作用下一對手性相反的狄拉克錐在倒空間被拉開的示意圖 圖3.兩種類型的外爾點周圍能帶
圖3.兩種類型的外爾點周圍能帶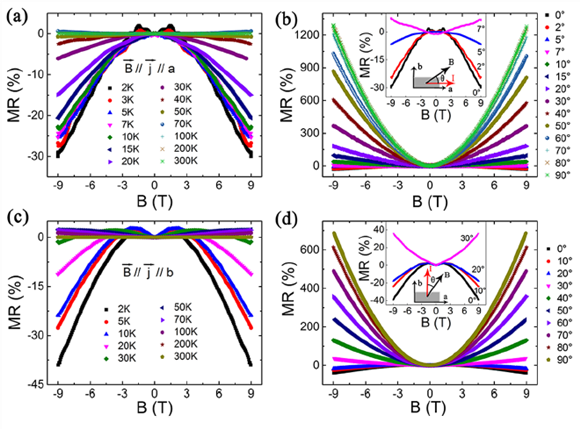 圖4.ABJ效應導致的負磁阻強烈依賴於溫度以及磁場和電場間的夾角
圖4.ABJ效應導致的負磁阻強烈依賴於溫度以及磁場和電場間的夾角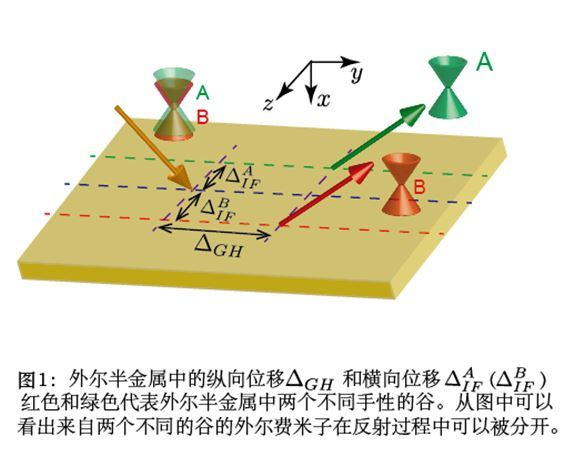 圖6
圖6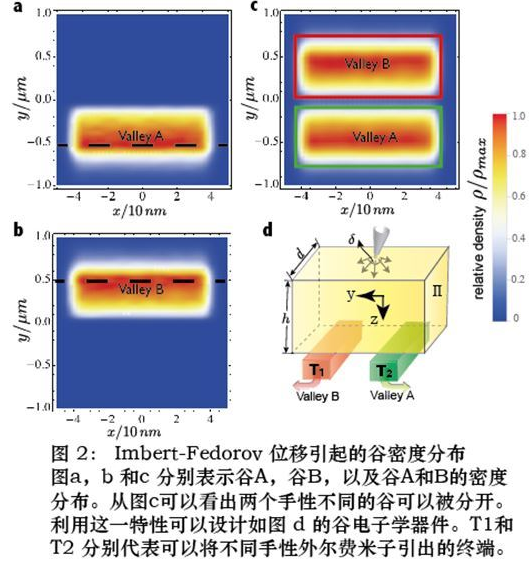 圖7
圖7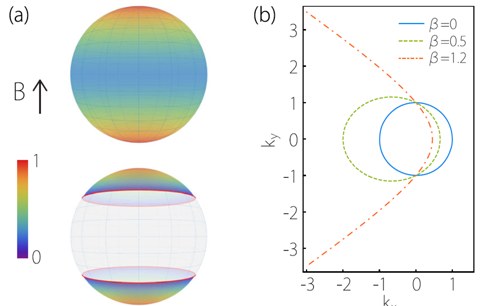 圖8
圖8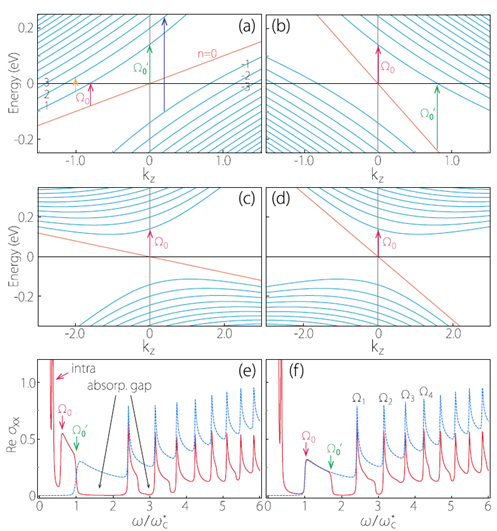 圖9
圖9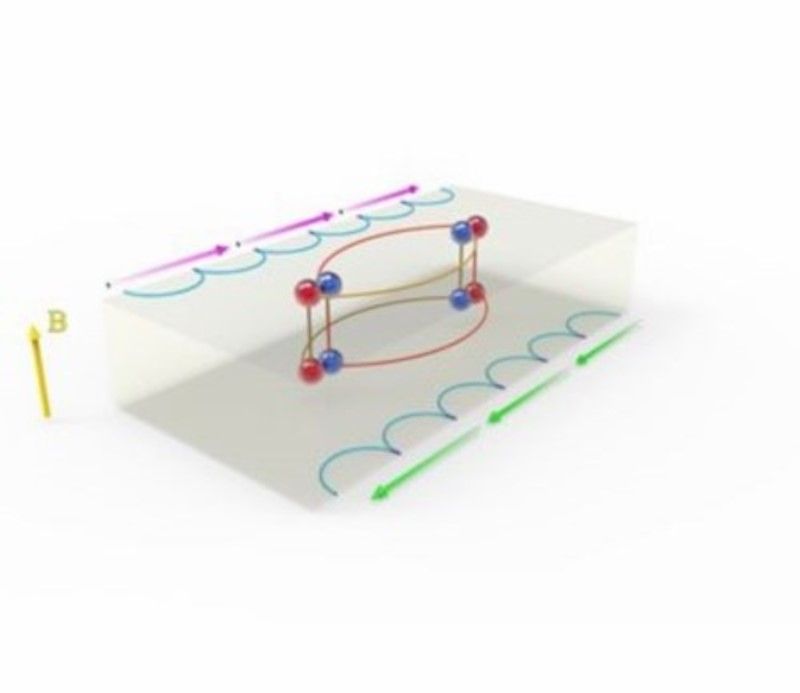
 圖1
圖1 圖2.在磁場作用下一對手性相反的狄拉克錐在倒空間被拉開的示意圖
圖2.在磁場作用下一對手性相反的狄拉克錐在倒空間被拉開的示意圖 圖3.兩種類型的外爾點周圍能帶
圖3.兩種類型的外爾點周圍能帶 圖4.ABJ效應導致的負磁阻強烈依賴於溫度以及磁場和電場間的夾角
圖4.ABJ效應導致的負磁阻強烈依賴於溫度以及磁場和電場間的夾角 圖6
圖6 圖7
圖7 圖8
圖8 圖9
圖9