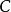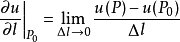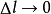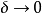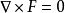定義
當研究物理系統中溫度、壓力、密度等在一定空間內的分布狀態時,數學上只需用一個代數量來描繪,這些代數量(即標量函式)所定出的場就稱為數量場,也稱標量場。最常用的標量場有
溫度場,電勢場,密度場,濃度場等等。
標量場的等值面
定義
令
,其中
是任意常數,則該式在幾何上表示一個曲面,在這個曲面上的各點,雖然坐標
不同,但函式值相等,稱此曲面為標量場
的
等值面。隨著
的取值不同,得到一系列不同的等值面。同理,對於由二維函式
所給定的平面標量場,可按
得到一系列不同值的等值線。
作用
標量場的
等值面或
等值線,可以直觀地幫助我們了解標量場在空間中的分布情況。例如,根據地形圖上等高線及其所標出的高度,我們就能了解到該地區的高低情況,根據等高線分布的疏密程度可以判斷該地區各個方向上地勢的陡度。
標量場的方嚮導數
定義
設
為標量場
中的一點,從
出發引出一條射線
,在
上
點附鄰取一點
,記線段
,如果當
時,
的極限存在,則稱它為函式
在點
處沿
方向的
方嚮導數,記作:
由此定義可知,方嚮導數是函式
在一點處沿某一方向對距離的變化率,故當
時,
沿
方向是增加的;當時
,
沿
方向是減少的。
方嚮導數的計算
標量場的梯度
定義
方嚮導數為我們解決了函式
在給定點處沿著某個方向的變化率問題。然而從場中的給定點
出發,標量場
在不同方向上的變化率一般來說是不同的,那么,可以構想,必定在某個方向上變化率為最大。為此,我們定義一個矢量
,其方向就是函式
在點
處變化率為最大的方向,其大小就是這個最大變化率的值,這個矢量
稱為函式
在點
處的
梯度,記為:
運算元
與標量函式
相乘為一矢量函式。在直角坐標系中,梯度又可以表示為:
另外,以後還會經常用到標量
拉普拉斯運算元,即:
。在直角坐標系中標量函式的拉普拉斯表達式為:
。
標量函式
在
圓柱坐標系中的梯度和拉普拉斯表達式分別為:
標量函式
在
球坐標系中的梯度和拉普拉斯表達式分別為:
性質
(2)標量場
中每一點
處的梯度,垂直於過該點的
等值面,且指向函式
增大的方向。也就是說,梯度就是該等值面的法向矢量。
(3)
,這個式子表明:如果有一個矢量場
滿足
,即
是一個
無旋場,則矢量場
可以用一個標量函式
的梯度表示,即
,該標量函式稱為
勢函式,對應的矢量場稱為有勢場。如靜電場中的電場強度就可以用一個
標量函式的梯度來表示。
標量場和矢量場
在一定的單位制下,用一個實數就足以表示的物理量是標量,如時間、質量、溫度等;在這裡,實數表示的是這些物理量的大小。
和標量不同,矢量是除了要指明其大小還要指明其方向的物理量,如速度、力、電場強度等;矢量的嚴格定義是建立在坐標系的
旋轉變換基礎上的。常見的矢量場包括Maxwell場、重矢量場。