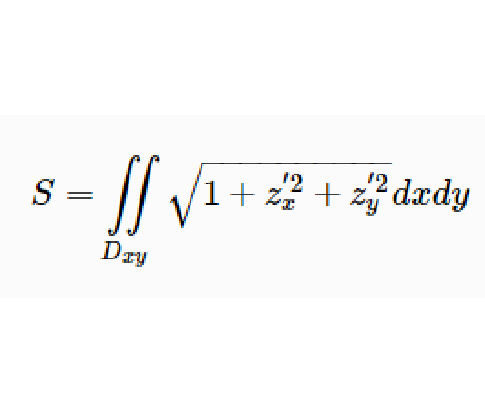曲面面積

曲面面積(area of a surface)是指曲面表面的面積。把光滑曲面S分成沒有公共內點的n塊S₁,... , S_n，且每一塊仍是光滑曲面，在每個S上取一點P，過P作S的切平面T，將s投影到T上，所有這些投影的面積之和的極限(當所有S的直徑趨於零時)如果存在，就是曲面S的面積，對有界簡單光滑曲面而言，這樣的極限總是存在的，而且與曲面的光滑等價的參數表示的選擇無關。

基本介紹

• 中文名：曲面面積
• 外文名：area of a surface
• 所屬學科：數學
• 相關概念：積分、面積微元、偏導數等

基本介紹

設空間有界曲面 為

其中 是 在 面上的投影區域， 在 上具有連續的偏導數，下面討論曲面的面積的計算問題。

現用平行於x軸和y軸的兩組平行直線分割投影區域 ，任取其中的一塊記作 ，其面積也記作 ，則當 的直徑很小時， 表示以 的邊界為準線，母線平行於z軸的柱面截得的曲面 上的那部分，設 是 上的任一點，根據條件，曲面 在點P處有切平面，則可用柱面截得切平面上的那一小片平面的面積dS近似地代替 的面積 ，則

其中， 是切平面與 面的夾角，也就是切平面的法向量n與 面的法線 軸的夾角，由曲面 的方程可知

所以

代人式(1)得

則曲面的面積微元為

將dS在投影區域 上積分，便得計算曲面面積的二重積分公式

如果所求曲面的方程用 或 表示比較方便，則同理可將曲面分別投影到 面或 面，類似地可得相應曲面的面積計算公式，分別為

或

其中， 分別為曲面 在yOz面或zOx面上的投影區域。

例題解析

例1 證明球面 的表面積為。

解: 由對稱性，取上半球面方程為 ，它在xOy面上的投影區域為

由式（2）得

例2 求拋物面位於之間的那一部分的面積。

解: 曲面在xOy面上的投影區域，由式(2)，得