基本介紹
- 中文名:區間套定理
- 外文名:theorem of nested interval
- 別稱:閉區間套定理
- 套用學科:數學
- 適用領域範圍:實數的完備性
- 屬性:實數集完備性的基本定理
定義





定理(閉區間套定理)

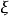


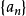
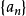
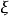









性質
推論






注


套用領域































區間套定理一般指本詞條






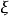


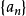
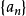
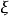




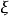












































閉區間套定理,是實數連續性的一種描述,幾何意義是,有一列閉線段(兩個端點也屬於此線段),後者被包含在前者之中,並且由這些閉線段的長構成的數列以О為極限,則這一列閉線段存在唯一一個公共點.定理定義 閉區間套 設有無窮多個...
閉區間的函式為小於等於的關係,即-∞≤a≤+∞,在數軸上為實心點。閉區間的余集(就是補集)是兩個開區間的並集。實數理論中有著名的閉區間套定理。代表符號:[x,y] ,即從x值開始到y值,包含x、y。比如:x的取值範圍是3到...
定理1(一元連續函式的有界性定理)若函式f在閉區間 上連續,則f在 上有界。證 套用區間套定理。假設函式f在閉區間 上無界。將區間 二等分,函式f必在 或 上無界,將函式f在其上無界的閉子區間記為 。如果函式f在這...
貝爾綱定理是點集拓撲學和泛函分析中的一個重要的工具。完備的度量空間必是第二綱集。簡介 貝爾綱定理斷言:完備的度量空間必是第二綱集。貝爾綱定理是區間套定理的發展與提高,在證明許多存在定理時是很有用的。這個定理有兩種形式,...
巨觀經濟區間數據泛論是一本2019年出版的圖書,由中國經濟出版社出版 內容簡介 本書依區間定理和區間套定理,研究和發現了我國新常態時期經濟發展的主要區間數據特徵,分析了我國主要十項巨觀經濟指標的合理運行區間的分布,它們的長度、...
半開半閉區間(Semi open closed interval)是高中數學中函式的一種定義域,常簡稱為“半開區間”或“半閉區間”。半開半閉區間用“( ]”表示。半開半閉區間與區間的其他兩種(開區間和閉區間)又稱為有界區間或有限區間,其他的...
證明:零點定理可以利用閉區間套定理:如果{[aₙ,bₙ]}是一個閉區間套,那么存在唯一實數ξ屬於所有的閉區間。詳細證法參考相應詞條。介值定理可以構造輔助函式來證明。令g(x)=f(x)-C,其中C是A和B之間的任一實數,則g(x)...
19世紀戴德金利用他提出的分割理論,從對有理數集的分割精確地給出了實數的定義,並且該定義作為現代數學實數理論的基礎之一可以推出實數理論中的六大基本定理:確界原理、單調有界定理、閉區間套定理、有限覆蓋定理、緻密性定理和柯西收斂...
具體來說,閉區間套定理和柯西收斂準則不能,其他5個基本定理則可以推出阿基米德公理。因此,以完備性公理作為實數公理之一時,阿基米德公理可以去掉;以5個可以推出阿基米德公理的基本定理替代完備性公理時,阿基米德公理也可以去掉;而以柯西...
6.6.1 區間套定理 148 6.6.2 區間套定理的運用 149 第7章纏論實戰之買賣點法則 7.1/ 第 一類買賣點 152 7.1.1 第 一類買點解析 153 7.1.2 第 一類賣點解析 155 7.2/ 第二類買賣點 157 7.2.1...
7.1 區間套定理 169 7.1.1 區間套的解讀 169 7.1.2 區間套縮小交易區間 171 7.2 日K線級別的纏論背馳 173 7.2.1 日K線回升趨勢纏論背馳 173 7.2.2 日K線回落趨勢纏論背馳 175 7.3 60分鐘級別背馳 177 7.3.1 60...
2.2 數列極限存在的條件.施篤茨定理 第三章 關於實數系完備性的基本定理 3.1 確界原理.區間套定理 3.2 聚點定理.有限覆蓋定理 3.3 數列的上、下極限 第四章 函式極限 4.1 函式極限的定義、性質與存在條件 4.2 兩個...
博雷爾清楚地認識到從一個區間的所有開覆蓋中能夠選出有限個覆蓋的重要性. 他完善了海涅(Heine)提出的覆蓋定理,即現在的所謂“海涅-博雷爾定理”或“有限覆蓋定理”,此定理和戴德金的“分割”法則、區間套定理、波爾察諾-魏爾斯特拉斯...
第七章 實數的完備性 1 關於實數集完備性的基本定理 一 區間套定理 二 聚點定理與有限覆蓋定理 三 實數完備性基本定理之間的等價性 2 上極限和下極限 第八章 不定積分 1 不定積分概念與基本積分公式 一 原函式與不定積分 二 ...
是一個閉區間套 由閉區間套定理,存在唯一實數 ,並且 ∴ 故數列 收斂,即級數 收斂。適用範圍 注意,萊布尼茨定理所給出的條件(1)是充分非必要條件,即對非單調遞減的數列{uₙ},交錯級數 既可能收斂,也可能發散。換句話說,...
一、 緻密性定理 二、 上、 下極限 §13.5 函式極限的歸結原則 §13.6 柯西收斂準則 一、 數列極限的柯西收斂準則 二、 函式極限的柯西收斂準則 三、 完備的距離空間 §13.7 區間套定理 §13.8 有限覆蓋定理 一、...
的閉區間 ,使 ;對 ,存在 中長度不超過 的閉區間 ,使 ;如此下去,得到一列閉區間,滿足:(1);(2) 的長度不超過 ,且 。因為 ,由數學分析中的閉區間套定理可知,存在唯一一點 。顯然有 ,由假設 應該是 中的...
§1 拉格朗日定理和函式的單調性 §2 柯西中值定理和不定式極限 §3 泰勒公式 §4 函式的極值與最大(小)值 §5 函式的凸性與拐點 §6 函式圖像的討論 §7 方程的近似解 總練習題 第七章 實數的完備性 §1 區間套定理·聚點...
實數具有完備性,本章涉及的實數理論的六個定理是數學分析理論的基石,是對極限理論的完善。課時 1. 區間套定理 2. 聚點定理 3. 有限覆蓋定理 4. 習題課 5. 上下極限概念 6. 上下極限性質 參考教材 “數學分析”慕課以華東師大...
3.1確界存在定理251 3.1.1用Dedekind基本定理證明確界存在定理251 3.1.2用確界存在定理證明Dedekind基本定理254 3.2單調有界定理255 3.3閉區間套定理256 3.4有限覆蓋定理258 3.5聚點原理264 3.6列緊性定理268 3.7Cauchy收斂準則...
2.3.5 閉區間上的連續函式的性質?習題2.3 第三章 實數及連續性 3.1 實數的基本定理 3.1.1 閉區間套定理 3.1.2 有限覆蓋定理 3.1.3 緻密性定理 習題3.1 3.2 實數系基本定理的等價性 習題3.2 3.3 實數系的連續性...
這裡把戴德金定理用作連續性公理。另一個常用作連續性公理的確界原理。公理組I~III與公理組I+II+(III)’是等價的,(注意不是III(III)’)。完備性公理可以換成閉區間套定理的形式。類似地,單調收斂定理,聚點原理等也可用作連續...
或第一綱集)。第二範疇集 度量空間的非第一範疇集稱為第二範疇集(或第二綱集)。性質 貝爾綱定理斷言:完備的度量空間必是第二範疇集。貝爾綱定理是區間套定理的發展與提高,在證明許多存在定理時是很有用的。
13.2.1 確界定理7 13.2.2 廣義實數系8 13.2.3 上極限和下極限9 習題13-215 13.3 實數連續性理論(二)16 13.3.1 柯西準則與區間套定理16 13.3.2 覆蓋與有限覆蓋17 習題13-321 13.4 R?n空間點集和多元函式的基本性質...
§3 確界存在定理與區間套定理 §4 緊性定理 §5 完備性定理 §6 連續函式性質證明 §7 壓縮映射原理 §8 上極限與下極限 第十章 反常積分 §1 無窮積分的概念 §2 無窮積分收斂性判別法 §3 瑕積分的概念 §4 瑕積分收斂性...
