基本介紹
定義

 | 如果  |
如果  ,且對於某個整數  | |
如果不存在整數 x,使得  。 |
公式
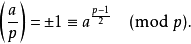
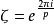

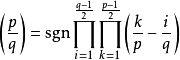
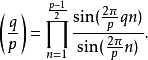
其它公式
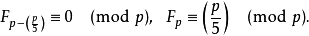


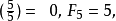
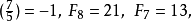

性質






計算例子




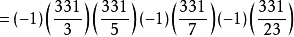



相關函式
- 雅可比符號是勒讓德符號的一個推廣,允許底數為合數,但底數仍然必須是奇數和正數。這個推廣提供了計算所有勒讓德符號的一個有效的方法。
- 一個進一步的推廣是克羅內克符號,把底數的範圍延伸到一切整數。


 | 如果  |
如果  ,且對於某個整數  | |
如果不存在整數 x,使得  。 |
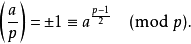
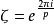

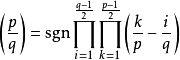
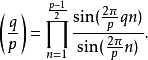
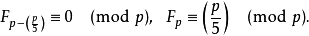


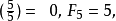
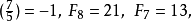











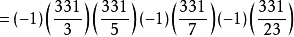



勒讓德符號,或二次特徵,是一個由阿德里安-馬里·勒讓德在1798年嘗試證明二次互反律時引入的函式。這個符號是許多高次剩餘符號的原型;其它延伸和推廣包括雅可比...
作為勒讓德符號的推廣,雅可比符號(Jacobi symbol)是Jacobi於1837年引入的一種數論符號。...
二次互反律漂亮地解決了勒讓德符號的計算問題,從而在實際上解決了二次剩餘的判別問題。歐拉和勒讓德都曾經提出過二次互反律的猜想。但第一個嚴格的證明是由...
儘管這種記號在某些方面來說十分簡潔,但現今最常用的是勒讓德符號,或稱二次特徵(見狄利克雷特徵)。對於整數a及奇質數p,如果p整除a; 如果a是模p的二次剩餘且...
儘管這種記號在某些方面來說十分簡潔,但現今最常用的是勒讓德符號,或稱二次特徵(見狄利克雷特徵)。對於整數a及奇質數p,如果p整除a; 如果a是模p的二次剩餘且...
0(mod 3),對每一個奇素數p,勒讓德符號時,p∤(a,b),這時方程y²=x³+kb²-k³a³無整數解。直到1875年,佩賓(T.Pepin)完整地證明了方程y²...
1878年,呂卡給出了一個判斷Mp是否為素數的方法:若有Δ>0,使勒讓德符號 ,且在二次域 中有一個單位數ε適合N(ε)=-1,則Mp為素數的充分必要條件是 。...
運用同餘性質和勒讓德符號可以加快檢驗速度。繼續算下去,可以得到:對於質數p =,(17/p) = +1(也就是說17是模這些質數的二次剩餘)。...
勒讓德符號: (a/p)=1 (相應的,-1) 如果 a是平方剩餘(相應的, 如果 a不是平方剩餘)。高斯著名的二次互反律告訴我們:假設p和q是2個不同的奇素數,則...
g有時被選擇成G的q階子群的生成元,而不是G本身的生成元,這樣g的勒讓德符號將不會顯示出a的低位。如果Alice和Bob使用的隨機數生成器不能做到完全隨機並且從...
是勒讓德符號,利用這個結果就較易得到某些大整數的一個素因子。例如,取P=4,Q=1,利用呂卡序列v0=2,v1=4,vn+2=4vn+1-vn。1930...
5. 2 勒讓德符號// 535. 3 雅可比符號// 565. 4 複合數模的情形// 59問題// 61計算題// 66第六章 元根和指數// 68...
若一個特徵對於所有與k互質的整數的值都為1,則稱為主特徵。 若p為素數,勒讓德符號(n|p)便是狄利克雷特徵的例子。狄利克雷特徵正文 編輯 數論...
1749年,歐拉(L.Euler)已給出了證明。近代有人把素數p=x²+y²中的x,y具體表示為p=(s(r)/2)²+(s(n)/2)²,其中r,n滿足勒讓德符號...
2 勒讓德符號3 高斯引理4 二次互反律5 二次剩餘理論套用舉例6 二次同餘式的解法和解數7 雅可比符號8 表素數為平方和9 表正整數為平方和第四章習題...
3.2 勒讓德符號543.3 高斯二次互反律573.4 雅可比符號583.5 二次同餘式的解法和解數63習題68第4章 原根和指數694.1 原根69...
是勒讓德符號。但是對於更一般的雅可比符號和希爾伯特符號也有對應的二次互反律。歐拉和勒讓德都曾經提出過二次互反律的猜想。但第一個嚴格的證明是由高斯在1796...
5.3 勒讓德符號 1885.4 雅可比符號 1985.5 模p平方根 2055.6 模數為合數的情形 2095.6.1 p為奇素數 2105.6.2 p=2 2105.7 解同餘方程小結 215...
17.勒讓德符號【表整數為平方和】18.二次互反律【n角形數與費爾馬】19.雅可比符號【阿達馬矩陣和猜想】20.合數模同餘【正十七邊形作圖法】伍n次剩餘...
若質數p大於5,且p整除,其中表示勒讓德符號,F(k)是第k個斐波那契數,則稱p為沃爾-孫-孫素數(Wall-Sun-Sun prime)。1960年,唐納德·丹斯·沃爾猜想是否存在這...
然後有時選擇g來生成G的階q子群而不是G,以便ga的勒讓德符號從不顯示a的低階位。使用這種選擇的協定例如是IKEv2。g通常是小整數,例如2.由於離散對數問題的...
7.1平方剩餘的基本概念7.2勒讓德符號7.3雅可比符號7.4模p平方根習題7第8章原根與離散對數8.1指數與原根8.2原根的存在性8.3離散對數8.4模冪算法習題8...
5. 3勒讓德符號 // 715. 4二次互反律 // 745. 5雅可比符號 // 77第二部分 基礎抽象代數——打開時代之門的鑰匙第六章 集合與二元運算 // 81...
4.2 勒讓德符號【表整數為平方和】 4.3 二次互反律【n角形數與費爾馬】 4.4 雅可比符號【阿達馬矩陣和猜想】 4.5 合數模同餘【正十七邊形作圖法】 習...
4.2 勒讓德符號4.3 二次同餘方程4.4 雅可比符號4.5 二次剩餘的套用習題四第5章 原根及其套用5.1 整數的階5.2 原根5.3 一般既約剩餘系的構造...
