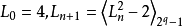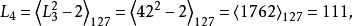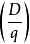呂卡序列

呂卡序列(Lucas sequence)是判定大素數的重要工具，法國數學家呂卡(Edouard Anatole Lucas，1842-1891)曾引進序列2，1，3，4，7，11，18，...，還得到其他一些菲波那契序列及它們所含數字間的關係。因此，不同於最早形式的那些菲波那契序列，有時也稱為呂卡序列。天文學家曾經注意到，日蝕和月蝕具有每6年，41年，47年， 88年，135年，223年和358年重複出現的模式。這些數構成一個呂卡序列。

基本介紹

• 中文名：呂卡序列
• 外文名：Lucas sequence
• 所屬學科：數學
• 所屬問題：初等數論(數論函式)
• 簡介：判定大素數的重要工具
• 提出者：法國數學家呂卡

基本介紹

設整係數一元二次方程x²-Px+Q=0，(P，Q)=1的兩根為α，β，則序列

和

稱為呂卡序列。這類序列在大整數的分解和解不定方程等方面都有用。

呂卡(Lucas, FrancoisÉdou-ard-Anatole1842-1891.10.3)是法國數學家。生於巴黎，卒於同地。早年畢業於亞眠(Amiens)師範學校。曾任天文台職員。在普法戰爭(1870-1871)中充當炮兵軍官。以後在巴黎兩所中學裡教學，致力於數論中素數理論和因子分解的研究。1876年設計新方法證明了2¹²⁷-1為一素數。此外，撰寫過四大卷本的《數學遊戲》(Re-creations mathematiques，1891-1894)，該書以問題新穎奇妙而盛行一時。

相關介紹

從定義可知序列(1)和(2)分別為以下整數序列：

和

序列(3)和(4)稱為循環序列。序列u_n和v_n還滿足以下諸關係式：

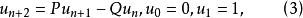
u_2n=u_nv_n；

；

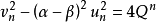
2u_m+n=u_mv_n+u_nv_m；

2v_m+n=Du_mu_n+v_mv_n，D=P²-4Q；

設素數p∤2Q，若u_l是序列u₁，u₂，…中能被p整除的足標最小的數，則p|u_n的充分必要條件是l|n。套用二次剩餘理論，呂卡序列在大整數的分解中有極重要的用途。設u_n是一個呂卡序列，若q是一個奇素數，且q∤Q，D=P²-4Q，則

其中 是勒讓德符號，利用這個結果就較易得到某些大整數的一個素因子。例如，取P=4，Q=1，利用呂卡序列v₀=2，v₁=4，v_n+2=4v_n+1-v_n。

1930年，萊默(D.H.Lehmer)給出了判別梅森數2^q-1是否為素數的一個有效方法：設q是一個奇素數，定義序列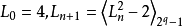，此處〈x〉_m表示x對模m的剩餘，則2^q-1是素數的充分必要條件是L_q-2=0。上述方法稱為萊默判別法。舉例說明如下：為了確定梅森數M₇=2⁷-1=127是否素數?設L₀=4，並通過公式計算L_i(i=0，1，2，…，5)之值，得序列：

由於L_q-2=L_7-2=L₅=0，故知M₇是素數。本例似乎並未顯示出萊默判別法的優越性，但在判定很大的梅森數時，如判定687位數字的梅森數M_{2 281}=2^{2 281}-1是否為素數時，即可顯示其重要作用，雖然M_{2 281}判定的計算量很大，但使用電子計算機來完成將是不困難的。事實上人們後來知道的那些更大的梅森素數，都是通過高速電子計算機採用此法來完成的。