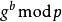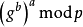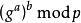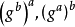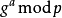迪菲-赫爾曼密鑰交換

迪菲-赫爾曼密鑰交換（英語：Diffie–Hellman key exchange，縮寫為D-H） 是一種安全協定。它可以讓雙方在完全沒有對方任何預先信息的條件下通過不安全信道創建起一個密鑰。這個密鑰可以在後續的通訊中作為對稱密鑰來加密通訊內容。公鑰交換的概念最早由瑞夫·墨克（Ralph C. Merkle）提出，而這個密鑰交換方法，由惠特菲爾德·迪菲（Bailey Whitfield Diffie）和馬丁·赫爾曼（Martin Edward Hellman）在1976年首次發表。馬丁·赫爾曼曾主張這個密鑰交換方法，應被稱為迪菲-赫爾曼-墨克密鑰交換（英語：Diffie–Hellman–Merkle key exchange）。

基本介紹

  • 中文名：迪菲－赫爾曼密鑰交換
  • 外文名：Diffie–Hellman key exchange
  • 提出時間：1976年
  • 套用學科：密碼學
  • 適用領域範圍：密碼學
  • 類型：安全協定
介紹,描述,歷史,安全性,身份驗證,參見,

介紹

迪菲-赫爾曼密鑰交換（英語：Diffie–Hellman key exchange，縮寫為D-H） 是一種安全協定。它可以讓雙方在完全沒有對方任何預先信息的條件下通過不安全信道創建起一個密鑰。這個密鑰可以在後續的通訊中作為對稱密鑰來加密通訊內容。公鑰交換的概念最早由瑞夫·墨克（Ralph C. Merkle）提出，而這個密鑰交換方法，由惠特菲爾德·迪菲（Bailey Whitfield Diffie）和馬丁·赫爾曼（Martin Edward Hellman）在1976年首次發表。馬丁·赫爾曼曾主張這個密鑰交換方法，應被稱為迪菲-赫爾曼-墨克密鑰交換（英語：Diffie–Hellman–Merkle key exchange）。
迪菲－赫爾曼密鑰交換的同義詞包括:
  • 迪菲－赫爾曼密鑰協商
  • 迪菲－赫爾曼密鑰創建
  • 指數密鑰交換
  • 迪菲－赫爾曼協定
雖然迪菲－赫爾曼密鑰交換本身是一個匿名（無認證）的密鑰交換協定，它卻是很多認證協定的基礎，並且被用來提供傳輸層安全協定的短暫模式中的前向安全性。

描述

迪菲－赫爾曼通過公共信道交換一個信息，就可以創建一個可以用於在公共信道上安全通信的共享秘密（shared secret）。
一般的描述:
愛麗絲和鮑伯寫上一個有限循環群G和它的一個生成元g。 （這通常在協定開始很久以前就已經規定好；g是公開的，並可以被所有的攻擊者看到。）
愛麗絲選擇一個隨機自然數a並且將
傳送給鮑伯。
鮑伯選擇一個隨機自然數b並且將
傳送給愛麗絲。
愛麗絲 計算
。
鮑伯 計算
。
愛麗絲和鮑伯就同時協商出群元素
，它可以被用作共享秘密。
因為群是乘法交換的。

歷史

迪菲－赫爾曼密鑰交換是在美國密碼學家惠特菲爾德·迪菲和馬丁·赫爾曼的合作下發明的，發表於1976年。它是第一個實用的在非保護信道中創建共享密鑰方法。它受到了瑞夫·墨克的關於公鑰分配工作的影響。約翰·吉爾（John Gill）提出了離散對數問題的套用。該方案首先被英國GCHQ的馬爾科姆·J·威廉森（Malcolm J. Williamson）在稍早的幾年前發明，但是GCHQ直到1997年才決定將其公開，這時在學術界已經沒有了研究這個算法的熱潮了。
這個方法被發明後不久出現了RSA，另一個進行公鑰交換的算法。它使用了非對稱加密算法。
2002年，馬丁·赫爾曼寫到：這個系統...從此被稱為“迪菲－赫爾曼密鑰交換”。 雖然這個系統首先是在我和迪菲的一篇論文中描述的，但是這卻是一個公鑰交換系統，是墨克提出的概念，因此如果加上他的名字，這個系統實際上應該稱為“Diffie–Hellman–Merkle密鑰交換”。我希望這個小小的講壇可以幫助我們認識到墨對公鑰密碼學的同等重要的貢獻。
描述了這個算法的美國專利 4,200,770，已經於1997年4月29日後過期，專利檔案表明了Hellman、Diffie和Merkle是算法的發明者。

安全性

在選擇了合適的G和g時，這個協定被認為是竊聽安全的。偷聽者（"Eve"）可能必須通過求解迪菲－赫爾曼問題來得到g。在當前，這被認為是一個困難問題。如果出現了一個高效的解決離散對數問題的算法，那么可以用它來簡化a或者b的計算，那么也就可以用來解決迪菲－赫爾曼問題，使得包括本系統在內的很多公鑰密碼學系統變得不安全。
G的階應當是一個素數，或者它有一個足夠大的素因子以防止使用Pohlig–Hellman算法來得到a或者b。由於這個原因，一個索菲熱爾曼素數q可以用來計算素數p=2q+1，這樣的p稱為安全素數，因為使用它之後G的階只能被2和q整除。g有時被選擇成G的q階子群的生成元，而不是G本身的生成元，這樣g的勒讓德符號將不會顯示出a的低位。
如果Alice和Bob使用的隨機數生成器不能做到完全隨機並且從某種程度上講是可預測的，那么Eve的工作將簡單的多。
秘密的整數a和b在會話結束後會被丟棄。因此，迪菲－赫爾曼密鑰交換本身能夠天然地達到完備的前向安全性，因為私鑰不會存在一個過長的時間而增加泄密的危險。

身份驗證

在最初的描述中，迪菲－赫爾曼密鑰交換本身並沒有提供通訊雙方的身份驗證服務，因此它很容易受到中間人攻擊。 一個中間人在信道的中央進行兩次迪菲－赫爾曼密鑰交換，一次和Alice另一次和Bob，就能夠成功的向Alice假裝自己是Bob，反之亦然。而攻擊者可以解密（讀取和存儲）任何一個人的信息並重新加密信息，然後傳遞給另一個人。因此通常都需要一個能夠驗證通訊雙方身份的機制來防止這類攻擊。
有很多種安全身份驗證解決方案使用到了迪菲－赫爾曼密鑰交換。當Alice和Bob共有一個公鑰基礎設施時，他們可以將他們的返回密鑰進行簽名，也可以像MQV那樣簽名g和g；STS以及IPsec協定的IKE組件已經成為了Internet協定的一部分；當Alice和Bob共享一個口令時，他們還可以從迪菲－赫爾曼算法使用口令認證密鑰協商，類似於ITU-T的建議X.1035。這已經被用作了G.hn的家庭網路標準。

參見

相關詞條

熱門詞條

聯絡我們