群中元素可以由最小數目個群元的乘積生成,這組群元稱為該群的生成元,生成元的數目為有限群的秩。
基本介紹
- 中文名:生成元
- 外文名:generator
- 所屬學科:數學
- 詞性:名詞
定義
生成子群
自由李代數
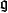
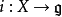
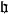
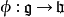
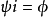
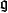
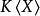
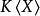
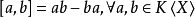
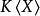
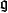
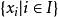

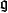
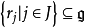
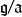
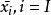
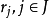

群中元素可以由最小數目個群元的乘積生成,這組群元稱為該群的生成元,生成元的數目為有限群的秩。
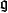
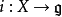
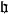
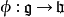
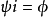
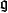
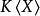
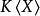
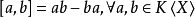
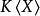
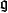
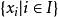

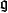
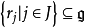
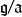
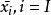
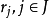
群中元素可以由最小數目個群元的乘積生成,這組群元稱為該群的生成元,生成元的數目為有限群的秩。...
施賴埃爾生成元(Schreier generators)有限表現群的一類特殊的生成元.設G一<g,,92,一gT,>,H是G中一個有限指數的子群,取定H在G中的一個右陪集完全代表系T....
定義介紹 生成元集(set of generators)布爾代數的特殊子集.令X是布爾代數B的子集,則X在B中生成子代數是 它是B的包含X的最小的子代數.如果XcA且(X)=A,則...
在數學中,表達式生成元、生成、由……生成、生成集合(generator, generate, generated by 與 generating set)可有許多緊密相關的技術性含義。...
《深層生成論》是2011年出版的圖書,作者是魯品越。...... 一 從構成論圖景到生成論機制 二 生成元與疊代方程:生成過程的結構 三 演化機制:從“生成元”到“吸...
19世紀末,由於幾何和拓撲研究的需要,無限群作為由一系列生成元及定義關係所定義的群出現。 有限生成群(finitely generated group)是無限群論研究的重要對象之一。指...
在抽象代數中,群 G 的生成集合是子集 S 使得所有 G 的所有元素都可以表達為 S 的元素和它們的逆元中的有限多個元素的乘積。...
對於線性空間V,dim span{a1,a2……an}=rank{a1,a2……an},也就是說span是線性空間V其中的一個最大無關組時,則稱該子空間為生成線性子空間。設向量組{α...
生成子群(generated subgroup)一類重要的子群...... 的生成元集,S中元為U的生成元.特別地,當G= (S>時,S中元稱為G的生成元.若S是有限集時,則稱G為有限生...
生成多項式就是用來把要進行防錯處理的二進制碼流進行轉換生成校驗碼,然後接收方會收到原始的二進制碼流和校驗碼,按照與傳送方相同的多項式再次進行轉換生成校驗碼,...
AG生成序列(AG generating sequence)有限可解群的一類特殊的生成元.若G是一個有限可解群,則G有一個合成群列G=GoDG}DGzD...DG,=1,其中G;-i /G; c yi...
強生成集(strong generating set)置換群計算的一個基本概念.設G是置換群,l} _甲i}}z}"..}風)為G的一個基.G中置換的一個子集s稱為關於B的一個強生成...
它們都是一種叫龐加萊群的李群的生成元,而龐加萊群是平移群與洛倫茲群的半直積。在這個群下不變的物件,可被稱為擁有龐加萊不變性或相對論性不變性。...
在數學中,Cayley圖,即凱萊圖,也叫做凱萊著色圖是編碼離散群的圖。它的定義是凱萊定理(以阿瑟·凱萊命名)所暗含的,並使用這個群的特定的通常有限的生成元集合。它...
無窮小運算元(infinitesimal operator)亦稱無窮小生成元,是隨機過程理論的重要概念,它可對任意巴拿赫空間上的任一運算元半群來定義,是由運算元半群決定的閉線性運算元。...
αm使得V的每一個向量均為這m個向量的線性組合,則V稱為數域P上的一個有限維向量空間,這時α1,α2,...,αm稱為V在P上的一組生成元,記作V=(α1,α2...
的生成元個數相加,就將得到 的元素總個數:n。也就是說:運用默比烏斯反演公式來“翻轉”這個和,就可以得到另一個關於元素個數的公式:其中μ 是所謂的莫比烏斯函...
