生成子空間

對於線性空間V，dim span{a1，a2……an}=rank{a1，a2……an}，也就是說span是線性空間V其中的一個最大無關組時，則稱該子空間為生成線性子空間。

設向量組{α₁，α₂，···，α_m}線上性空間V中，由它們的一切線性組合生成的子空間：

Span{α₁，α₂，···，α_m }=L(α₁，α₂，···，α_m)

= {k₁α₁+k₂α₂+···+k_mα_m| k_i}

基本介紹

• 中文名：生成子空間
• 外文名：generating subspace
• 表達式：Span{a1，a2……an}
• 適用領域範圍：線性代數、矩陣論
• 學科：數理科學
• 特性：重要的子空間

定義

設 是Rⁿ中任一組向量。記 的所有線性組合的集合為 ，即

稱 為向量組 生成的子空間。

定理

1.設 是Rⁿ中任一組向量。則 是Rⁿ的一個子空間。

2.設W是Rⁿ的一個子空間， 是W中一組向量，Span（α_1，α_2，```，α_m）⊆ W。

3.推論：設W是Rⁿ的一個子空間， 是W中一組向量，Span（α_1，α_2，```，α_m）= W的充分必要條件：W每個向量可以 線性表出。即Rⁿ的一個子空間的一組向量可以線性表出這個子空間的每個向量，那么這個子空間與子空間內的這一組向量的生成子空間是等價的。

當Span（α_1，α_2，```，α_m）= W時，稱 是子空間W的一組生成元。

重要性質

1）如果α₁，α₂，···，α_m線性無關，則其為生成子空間Span{α₁，α₂，···，α_m }的一組基；

2）如果α₁，α₂，···，α_r是向量組α₁，α₂，···，α_m的最大線性無關組，則

1.Span{α₁，α₂，···，α_m }= Span{α₁，α₂，···，α_r}

2.α₁，α₂，···，α_r是Span{α₁，α₂，···，α_m }的一組基

證明

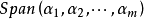1.： ，從而 非空。

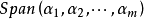
任取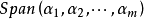 的兩個元素：

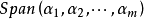
有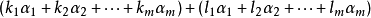

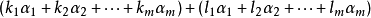
和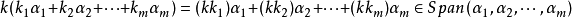

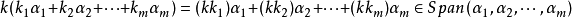
可推出非空，和線性運算封閉。故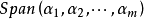 是Rⁿ的一個子空間。

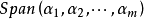
2.由向量子空間的定義：Rⁿ中任意向量的線性組合包含於W（是W中的元素），而 一是Rⁿ中任一組向量，它的線性組合即生成的子空間Span（α_1，α_2，```，α_m）也是包含於W的。

3.由定理2，Span（α_1，α_{2，```，</sub>α<sub>m</sub>）⊆ W。證明Span（α<sub>1，</sub>α<sub>2，```，}α_m）= W，只需證明Span（α_1，α_2，```，α_m）⊇W。

由條件， ，α可由α_1，α_{2，```，</sub>α<sub>m</sub>線性表出，α∈Span（α<sub>1，</sub>α<sub>2，```，}α_m），由於α的任意性，Span（α_1，α_{2，```，</sub>α<sub>m</sub>）⊇W也成立。故得Span（α<sub>1，</sub>α<sub>2，```，}α_m）= W。