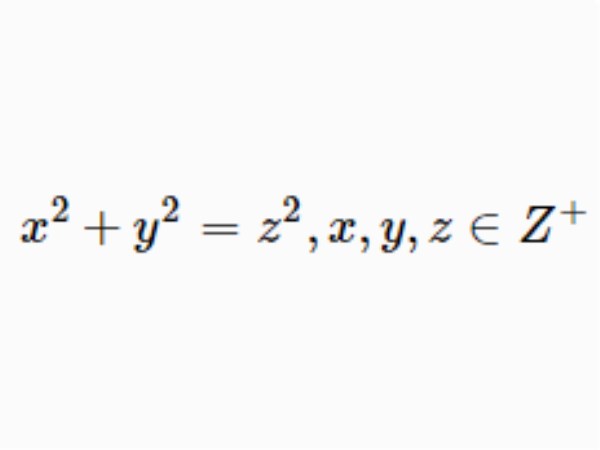基本介紹
- 中文名:畢達哥拉斯三元數組
- 外文名:Pythagorean triple
- 別稱:勾股數組,商高數組
- 所屬學科:數學
- 所屬問題:初等數論(不定方程)
基本介紹,本原畢達哥拉斯三元數組,相關介紹,
基本介紹
畢達哥拉斯三元數組(Pythagorean triple)亦稱勾股數組,又稱商高數組,是一個著名的不定方程問題,指三元二次不定方程的正整數解。若正整數x,y,z能使x2+y2=z2成立,則(x,y,z)是一個畢達哥拉斯三元數組。
本原畢達哥拉斯三元數組
當(x,y,z)=1時,則稱(x,y,z)為本原畢達哥拉斯三元數組。找出所有畢達哥拉斯三元數組就等同於求出不定方程

1.若(x,y,z)是滿足方程(1)的本原畢達哥拉斯三元數組,則x,y中有且僅有一數為偶數。因此,z必為奇數。
2.若(x,y,z)是滿足方程(1)的本原畢達哥拉斯三元數組,且設x為偶數,則存在正整數m和n,m>n,(m,n)=1,m n(mod 2),能使x=2mn,y=m2-n2,z=m2+n2成立。
n(mod 2),能使x=2mn,y=m2-n2,z=m2+n2成立。

3.若x=2mn,y=m2-n2,z=m2+n2,則(x,y,z)是滿足方程(1)的畢達哥拉斯三元數組。如果還有m>n>0,(m,n)=1和m n(mod 2),則(x,y,z)是本原畢達哥拉斯三元數組。
n(mod 2),則(x,y,z)是本原畢達哥拉斯三元數組。