基本介紹
- 中文名:分式線性變換
- 外文名:linear fractional transformation
- 所屬學科:數學(複變函數)
- 相關概念:保角變換、分時線性函式等
基本介紹
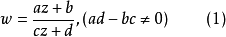
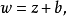
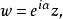
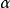
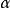
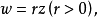
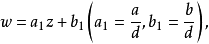
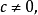
分式線性變換的性質
定理1
定理2
定理3
定理4

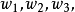

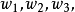
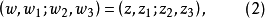
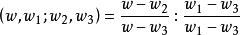
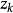
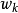
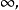
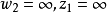
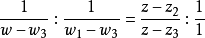
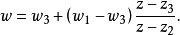

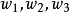
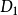
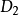
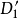
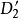
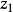
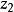
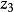
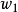
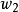
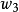
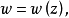
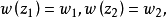
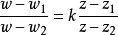
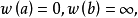
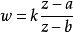

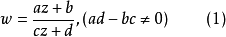
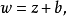
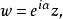
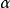
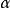
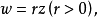
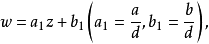
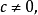
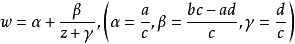

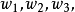

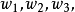
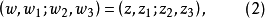
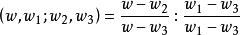
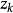
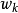
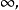
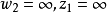
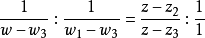
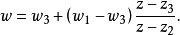

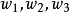
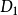
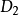
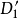
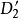
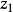
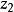
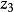
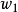
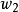
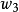
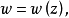
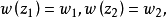
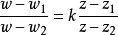
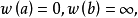
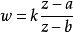
給定滿足條件ad-bc≠0的四個復常數a,b,c,d,把由函式w=f(z)=(az+b)/(cz+d)定義的變換稱為分式線性變換,定義中的條件ad-bc≠0 是為了保證變換的保角...
a,b,c,d都是實數且滿足ad-bc>0的分式線性變換稱為富克斯變換。富克斯變換將上半平面映為上半平面,使Ox軸(z=x+iy)上各點z與Ou軸(w=u+iv)上各點w對應...
透視變換是中心投影的射影變換,在用非齊次射影坐標表達時是平面的分式線性變換。透視變換常用於,例如在移動機器人視覺導航研究中,由於攝像機與地面之間有一傾斜角,...
變換.克雷蒙納變換構成的群稱為克雷蒙納群,記為Cr (P約.當n=2時,除了射影變換外最簡單的克雷蒙納變換是二次變換,它在非齊次坐標下可寫成以下的分式線性變換...
默比烏斯變換是以數學家奧古斯特·費迪南德·莫比烏斯的名字命名的,它也被叫做單應變換(homographic transformation)或分式線性變換(linear fractional transformation)。...
交比亦稱非調和比。是分式線性變換的一種不變數。在分式線性變換下任意四點的交比不變,換句話說,交比是線性變換的不變數。...
Pfaff 變換和 Euler 變換都是分式線性變換的例子,這得名於等式兩邊的超幾何函式的宗量的聯繫,參見莫比烏斯變換。將上面提到的四個連線關係與 Pfaff 變換及 Euler ...
6.2分式線性變換 6.3黎曼映射定理 習題六 第7章調和函式 7.1調和函式的定義及其性質 7.2泊松積分與狄利克雷問題 習題七 第8章解析開拓 8.1對稱...
2.分式線性變換3.某些初等函式所構成的共形映射4.關於共形映射的黎曼存在定理和邊界對應定理第七章習題第八章解析延拓1.解析延拓的概念與冪級數延拓...
全書共分八章,內容包括;複平面,擴充複平面,解析函式,分式線性變換,Cauchy定理,Cauchy公式,冪級數,最大模原理,Schwarz引理,Laurent級數,留數及其套用,調和函式,解析...
7.2 分式線性變換(映射)7.3 若干類初等函式所構成的保形(共形)映射7.4 保形映射的黎曼存在定理與邊界對應定理7.5 若干個值分布研究中的不等式*習題7...
7.1共形映射的概念7.2分式線性變換7.3一些初等函式所構成的共形映射習題7部分習題答案參考文獻參考資料 1. 複變函數 .清華大學出版社[引用日期2015-08-19] ...
習題52.3 分式線性變換A.分式線性函式B.對稱C.交比習題2.4 級數A.複數項級數B.函式項級數C.冪級數D.指數函式與三角函式習題第3章 復積分...
把分式線性變換擴充到複數域上,得到了Klein群用新的自守函式理論來解決僅有正則奇點的任意階具有代數係數的常微分方程用自守函式理論導出一般的單值化定理...
φ=ƒ 的共形映射φ(叫做覆蓋變換)組成一個富克斯群。因此,除去上面幾種特例外,每一個黎曼曲面都可表示成單位圓關於一個富克斯群的商;因而,分式線性變換組成的...
2.分式線性變換3.某些初等函式所構成的共形映射4.關於共形映射的黎曼存在定理和邊界對應定理第七章習題第八章解析延拓1.解析延拓的概念與冪級數延拓...
6.2 分式線性變換6.3 某些初等函式所構成的共形映射習題六第二部分 數學物理方程符號說明表第七章 數學物理方程的導出和基本概念7.1 數學物理方程的導出...
交比與分式線性變換龐加萊模型中的非歐距離羅巴切夫斯基幾何的實現從非歐幾何到黎曼幾何五、結束語參考文獻參考資料 1. 並不神秘的非歐幾何 .豆瓣[引用日期2017-...
也可用一分式線性變換t=ω(z),|z|<1,把z變到t平面的上半平面,使A,B,C 分別變成實軸的α,b以及 ,而 變成區域 (圖2),當 關於其一邊界圓弧作對稱反演...
5 分式線性變換6 等速圓周運動習題解答或提示14冊1 什麼是單位分數2 一個古老的傳說3 鑲地板和鋪路4 把真分數表成單位分數的和...
