基本介紹
- 中文名:反演變換
- 外文名:inversion
- 學科:數學
- 特點:兩個圖形相反
- :
- :
數學反演變換
定理一
定理二
作已知點的反演點的方法
圓的反演變換
性質
畫圖
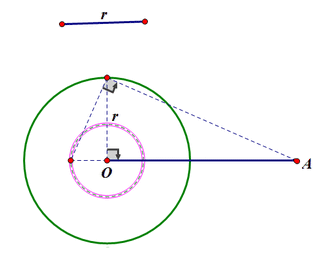 圖1 畫反演圓的反演中心
圖1 畫反演圓的反演中心 圖2 反演成像
圖2 反演成像 圖3 圓在不同情況下的反演成像
圖3 圓在不同情況下的反演成像 圖5作點的反演變換
圖5作點的反演變換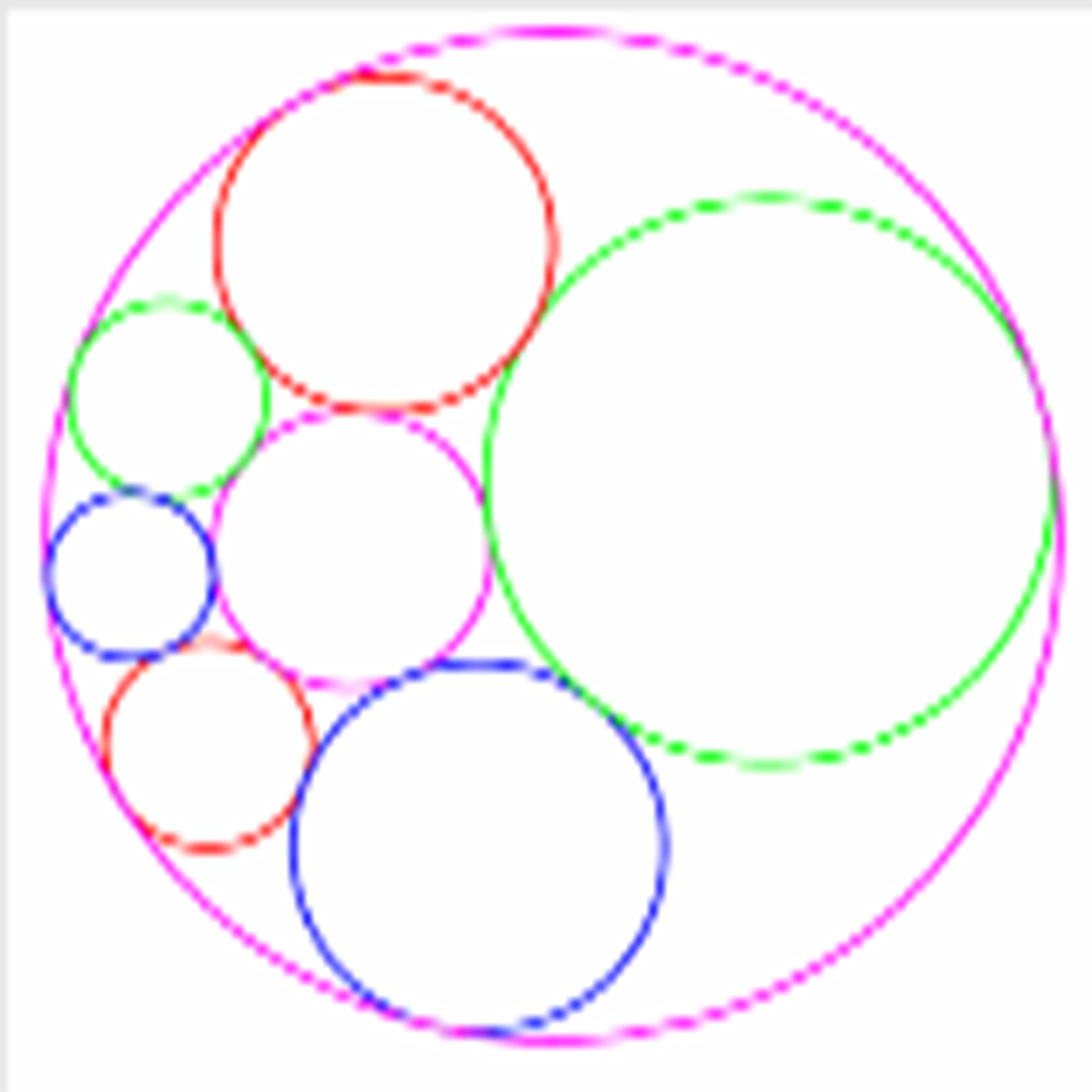
 圖1 畫反演圓的反演中心
圖1 畫反演圓的反演中心 圖2 反演成像
圖2 反演成像 圖3 圓在不同情況下的反演成像
圖3 圓在不同情況下的反演成像 圖5作點的反演變換
圖5作點的反演變換設在平面內給定一點O和常數k(k不等於零),對於平面內任意一點A,確定A′,使A′為直線OA上一點,並且有向線段OA與OA′滿足OA·OA′=k,我們稱這種變換是以O...
橢圓型反演變換(elliptic inversion transformation)是反演變換的一,指反演冪k<0的反演變換。根據反演變換的定義及任何一個實數的平方不會是一個負數,橢圓型反演變換...
雙曲型反演變換是反演變換的一種,指反演冪k>0的反演變換,這時k可表為k=r2(r>0),r稱為反演半徑,通常稱雙曲型反演變換為關於反演基圓(球)的反演變換。...
反演法作圖(construction by inversion trans-formation)是解作圖題的一種特殊方法,就是利用反演變換的性質(如過反演中心的圓變為直線,保角性等)來解作圖題的方法...
本書從平面幾何對稱的知識出發,介紹反射變換的概念、性質和它在幾何極值問題、等周問題、光的傳播原理等方面的有趣套用;在此基礎上引出一般平面變換的概念,介紹平移...
初等幾何變換,是一個將幾何圖形按照某種法則或規律變成另一種幾何圖形的過程。它對於幾何學的研究有重要作用。初等幾何變換主要包括全等變換,相似變換,反演變換。...
《反射與反演》是2013-1出版的圖書,作者是嚴鎮軍。...... 一般平面變換的概念,介紹平移變換、旋轉變換和相似變換在證明幾何題方面的套用;然後介紹一種反演變換及其應...
默比烏斯變換(Mobius transformation),也稱莫比烏斯變換,是數論中的一種重要變換。默比烏斯變換是以數學家奧古斯特·費迪南德·莫比烏斯命名的, 它也被叫做homographic ...
宇稱(yǔ chèn),描述粒子在空間反演下變換性質的相乘性量子數,引記為P。它只有兩個值+1和-1。如果描述某一粒子的波函式在空間反演變換(r→-r)下改變符號,...
在量子力學中,量子系統中的粒子存在運動上反演的性質,稱為時間反演對稱性。對於時間反演對稱性,對應著存在反么正算符。反么正算符即反線性的么正算符。...
幾何變換是把一個幾何圖形按照某種法則或規律變成另一種圖形的過程。因為幾何圖形都是點的集合,所以幾何變換都是通過點的變換實現的。位似變換是一種幾何變換。設O...
在熱力學領域中,不可逆過程是相對可逆過程而言的,指的是在時間反演變換下只能單向進行的熱力學過程,這種熱力學過程所具有的性質被稱作不可逆性(irreversibility)。從...
