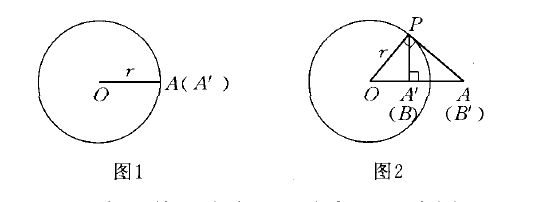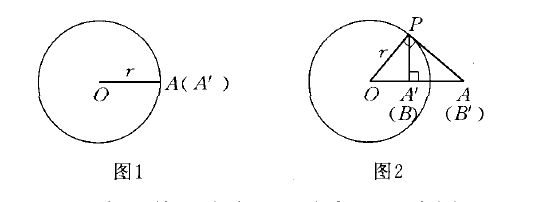雙曲型反演變換是反演變換的一種，指反演冪k>0的反演變換，這時k可表為k=r2(r>0)，r稱為反演半徑，通常稱雙曲型反演變換為關於反演基圓（球）的反演變換。
基本介紹
- 中文名：雙曲型反演變換
- 外文名：hyperbolic inversion transformation
- 適用範圍：數理科學
公式簡介,反演基圓,求反演點,
公式簡介
雙曲型反演變換是反演變換的一種，指反演冪k>0的反演變換，這時k可表為k=r2(r>0)，r稱為反演半徑。
反演基圓
以反演中心O為圓（球）心，以反演半徑r為半徑作圓（球），根據反演變換的定義，此圓（球）上的點的反演點是它自身，這樣的點稱為反演變換的二重點，並將此圓（球）稱為反演基圓（球）。由於這個圓的存在，因而通常稱雙曲型反演變換為關於反演基圓（球）的反演變換。
只要給定反演中心O和反演冪k>0，這個雙曲反演變換就是確定的，因而對於平面上（空間中）的非反演中心的任意一點A，都可利用幾何作圖求出其反演點A'。
求反演點
求反演點的方法：
首先以O為圓心，以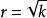
為半徑作反演基圓。
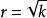
1.若A點在⊙O(r)上，則點A'與點A重合（如圖1）。
2.若A點在⊙O(r)外，從A點向⊙O(r)作一條切線，切點為P，從P點引OA的垂線，垂足即為A'（如圖2）。
3.若B點在⊙O(r)內，則與2的作圖相反，即過B點作OB的垂線交⊙O(r)於點P，過P點作⊙O(r)的切線交OB的延長線於B'點，B'即為B的反演點（如圖2）。
