基本介紹
- 中文名:反演法作圖
- 外文名:construction by inversion trans-formation
- 所屬學科:數學
- 所屬問題:平面幾何(尺規作圖)
- 簡介:利用反演變換的性質解作圖題
基本介紹
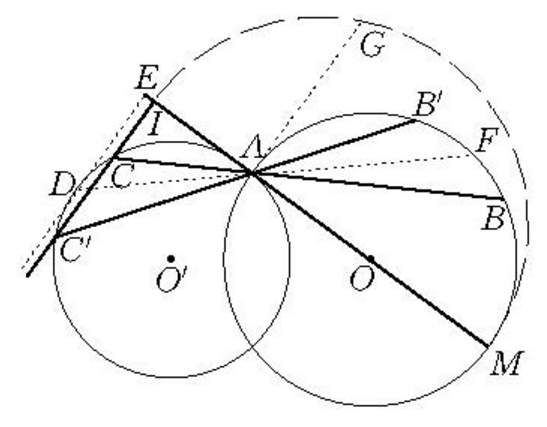 圖1
圖1例題分析
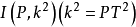
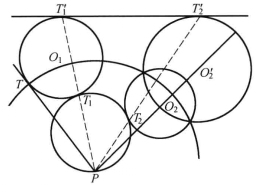 圖2
圖2 圖3
圖3
 圖1
圖1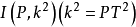
 圖2
圖2 圖3
圖3反演法作圖(construction by inversion trans-formation)是解作圖題的一種特殊方法,就是利用反演變換的性質(如過反演中心的圓變為直線,保角性等)來解作圖題的方法...
反演法,是一種套用於數學與計算機科學的技術。...... 反演法,是一種套用於數學與計算機科學的技術。...又稱“伴隨系統法”、“對偶系統法”、“共軛系統法...
反演變換畫圖 1.首先約定,反演圓的圓心O是反演中心。規定反演半徑就是反演圓的半徑r(在解題和具體的套用上,可以用不同的反演半徑,不必非得是反演圓的半徑)。再...
散射反演法(scattering inversion method)是指求解具有孤立子解的特殊非線性方程的一種方法。...
《反演問題的計算方法及其套用》適合於數學物理專業的科研人員、大學教師使用,又可以作為相關專業研究生和高年級大學生的教材,亦可供從事科學和工程領域中反問題(比如...
遙感反演參數同化法(初始化/參數化法),是將遙感反演的狀態變數(LAI、TS、WS 等)與模型模擬值進行對比,構建代價函式,並採用最佳化算法調整模型的初始條件(初始值)或...
只要給定反演中心O和反演冪k>0,這個雙曲反演變換就是確定的,因而對於平面上(空間中)的非反演中心的任意一點A,都可利用幾何作圖求出其反演點A'。...
反演問題的計算方法及其套用內容簡介 編輯 第一部分介紹基本概念和事例;第二和第三部分分別研究線性反問題的計算方法和典型套用;第四和第五部分研究非線性反問題的...
編幾何作圖題解法及其原理,第三編初第幾何學作圖不能問題,第四編幾何作圖題及...第五章 幾何變換 反演第六章 用他種工具作圖法Mascheroni單用圓規作圖法...
余凡,中國測繪科學研究院副研究員,主要研究方向為攝影測量與遙感,,成功申請獲批國家自然科學基金面上項目“利用全極化SAR數據反演地表土壤水分方法研究”(41471299),...
本書共分五編,分別為第一編近世幾何學初編,第二編幾何作圖題解法及其原理,...第五章 幾何變換 反演第六章 用他種工具作圖法Mascheroni單用圓規作圖法...
由於開發地震反演成果是惟一的, 屬於確定性建模範疇。(三) 計算機插值建模目前油田上流行的計算機地質繪圖軟體, 基本上屬於確定性內插建模技術。儘管插值的方法很多,...
