基本介紹
- 中文名:正六邊形
- 來源:平面幾何
- 性質:6個角相等,6條邊相等
- 劃分:6個全等的正三角形
- 高:√3a
- 正六邊形面積:(3/2)×√3a2
性質,尺規作圖,常見圖形,雪晶,蜂巢,
性質
因為是正六邊形,正六邊形就可以分成過中心6個全等的正三角形,作正三角形的高,利用勾股定理可求高為√3/2×a,每個三角形的面積都是√3/4×a2,所以正六邊形的面積為(3/2)×√3a2(其中a為邊長)(如下圖)。
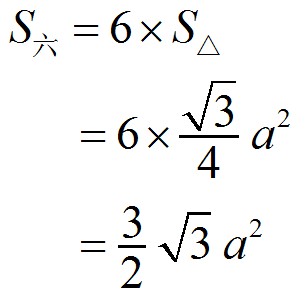
尺規作圖
方法一:作圓,以半徑為長度單位(半徑即是所求正六邊形邊長),劃分圓,並連線各分點,即是所求正六邊形。

方法二:
以任意長畫一條線段AB。以A為圓心,AB為半徑,作圓A。以B為圓心,AB為半徑,作圓B與圓A交於點C。連線AC,BC。三角形ABC為等邊三角形。在AB上取三等分點M。在AC和BC上分別取點N,O,使CN=AM=OB。作MX平行於BC,交AC於點X。作NY平行於BA,交BC於點Y。作OZ平行於AC,交AB於點Z。
則NYOZMX為正六邊形。
方法三:
畫一個圓,做其一條直徑。以直徑的兩個端點為圓心,以已做圓的半徑為半徑分別畫圓,做出4個交點,依順序聯結這4個點和直徑的兩個端點就可以。正6邊形中間一點0,過0做正6邊形任意一條邊的垂線,然後用這條邊的長乘以垂線的長,得出數字來把數字除以2,再乘以6。 雪花
雪花
 雪花
雪花常見圖形
雪晶
雪晶的六角形狀能細分為兩大類,一是片狀,另一類是柱狀。經常看到比較美麗的雪花便是那些六邊對稱的片狀雪晶。它們通常會在溫度介乎攝氏零下五度至零下二十度之間形成,柱狀雪花包括了針狀和中空柱狀,針狀雪晶在溫度介乎攝氏零度至攝氏零下五度形成,中空柱狀在是低於攝氏零下二十度形成。
如果希望找出大部分冰晶是六角稜體的原因,或許應該首先了解一下水分子。水分子是由兩個氫原子以及一個氧原子(這便是我們常把水稱為H2O的原因),它們以一種很強的鍵——共價鍵, 黏合在一起。
當液態的水分子被冷卻至凝固點,水分子會互相碰撞,形成固態冰晶,然後它們會利用氫鍵結合在一起。若分子與分子之間結合,便會更穩定。相對來說,最穩定的排列方式是以六角形狀把六個水分子黏在一起,這也是為什麼大部份冰晶是六角形的。

 蜂巢
蜂巢