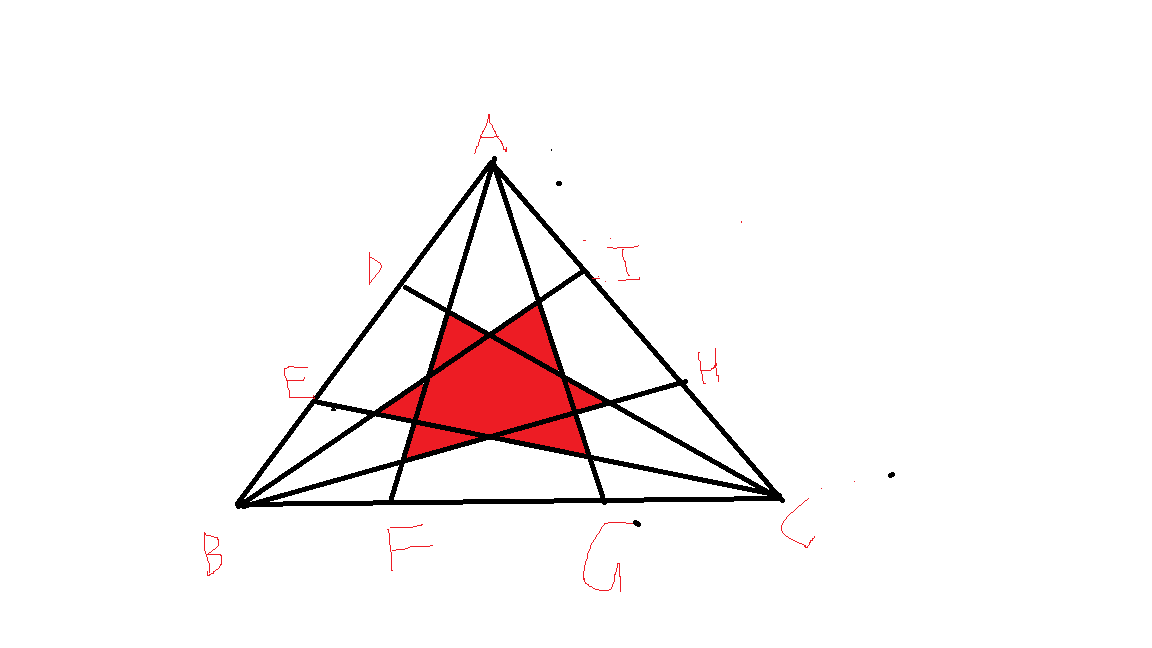三等分點(Three equal points)是把一條線段平均分成三等分的點。以該線段為中線做一任意三角形,畫出三角形的另一條中線,那么兩中線交於點A,以該點為圓心,該線段到三角形底邊的距離為半徑作圓,交於該線段於點B,則點A,B就是該線段的三等分點。
基本介紹
- 中文名:三等分點
- 外文名:Three equal points
- 作用:一條線段平均分成三等分兩個點
- 性質:數學名詞
- 提出:1821年
- 地點:中國
釋義,三角形性質,方法(尺規做三等分點),方法一,方法二,方法三,相關概念(等分圓周),
釋義
把一條線段平均分成三等分的兩個點,都叫線段的三等分點。
三角形性質
三角形中線的交點到底邊中點的距離是中線的三分之一。
方法(尺規做三等分點)
以該線段為中線做一任意三角形,畫出三角形的另一條中線,那么兩中線交於點A,以該點為圓心,該線段到三角形底邊的距離為半徑作圓,交於該線段於點B,則點A,B就是該線段的三等分點。
方法一
已知AB線段,做AB為底的等邊三角形,做AB的垂直平分線,設上面一點是C,再做BC的垂直平分線,兩平分線相交D吧,設AB中點為E,那么DE是EC的三分之一,延長CE,然後取EF等於ED,可以看出三角形ADF是等邊三角形,做AD的垂直平分線,交AE於一點,設為G,AG就是AB的三分之一,如上做另一邊的三分之一,即可。
方法二
把已知線段的一個端點作為頂點,任意作延長線,在延長線上從頂點開始任意截取相等的連續的三段,形成另一條線段,然後把已知線與你作的線段的另一個端點相連,形成三角形,過三等分點做底邊的平行線,交已知線段上的點就是所要的三等分點。
方法三
已知線段AB,將AB線段四等分,分別為A,C,D,E,B。以ACD為直徑畫圓,再以CDEB為直徑畫圓,兩圓交點為點F,過F點作AB的垂線交AB於點F,點F即為線段AB的三等分點。
相關概念(等分圓周)
等分圓周(circumference in equal parts),圓內接正多邊形的作圖問題,若圓周上依次有n個點A1,A2,A3,…,An(n≥2),把整個圓周分成n段相等的弧: