基圓指的是在凸輪中以凸輪輪廓最小向徑為半徑所作的圓。最短向徑即為基圓半徑。
基本介紹
- 中文名:基圓
- 外文名:bace circle
- 所屬學科:數理科學
- 相關概念:基圓半徑、凸輪等
定義
基圓半徑的大小對凸輪機構的影響
凸輪基圓半徑的確定
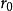
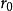
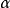
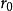
凸輪機構壓力角α與基圓半徑的關係
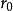
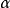
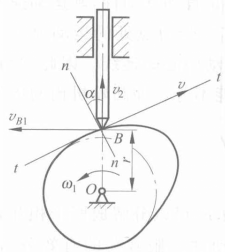 圖1(a) 從動件運動速度分析
圖1(a) 從動件運動速度分析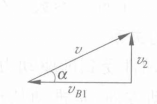 圖1(b)從動件運動速度分析
圖1(b)從動件運動速度分析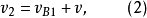

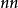
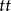

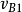
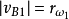

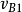

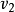

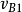

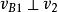

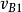
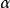

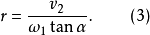
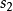
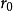
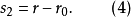
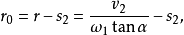

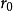
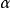
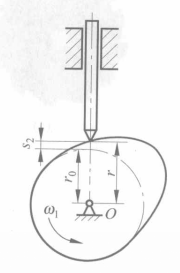 圖2
圖2確定凸輪基圓半徑
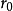
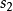
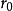
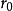
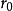
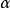
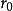

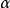
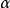
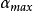
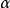
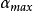
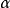
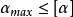
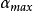
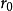
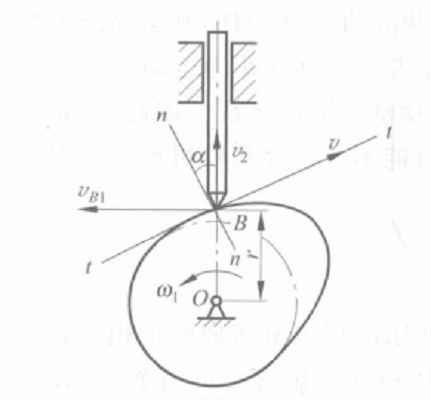
基圓指的是在凸輪中以凸輪輪廓最小向徑為半徑所作的圓。最短向徑即為基圓半徑。
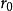
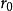
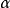
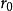
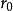
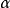
 圖1(a) 從動件運動速度分析
圖1(a) 從動件運動速度分析 圖1(b)從動件運動速度分析
圖1(b)從動件運動速度分析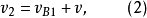

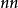
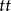

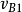
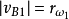

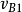

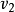

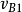

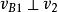

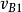
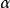

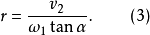
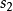
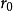
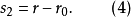
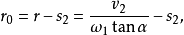

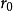
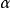
 圖2
圖2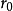
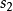
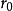
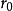
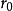
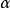
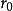

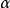
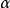
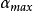
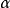
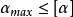
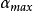
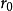
基圓指的是在凸輪中以凸輪輪廓最小向徑為半徑所作的圓。最短向徑即為基圓半徑。...... 基圓指的是在凸輪中以凸輪輪廓最小向徑為半徑所作的圓。最短向徑即...
基圓直徑=分度圓直徑×分度圓壓力角的餘弦。...... cos20°=0.9397,基圓直徑=75×cos20°=70.48mm詞條標籤: 文化 V百科往期回顧 詞條統計 瀏覽次數:次 ...
基圓半徑通常是指凸輪的理論廓線的最小半徑。基圓半徑也是凸輪設計的一個重要參數,它對凸輪機構的結構尺寸、體積、重量、受力狀況和工作性能等都有重要影響。...
齒輪基圓 (英文:gear base circle)是指漸開線圓柱齒輪(或擺線圓柱齒輪)上的一個假想圓,形成漸開線齒廓的發生線(或形成擺線齒廓的發生圓)在此假想圓的圓周上作...
基圓柱是由基圓擴展形成的,齒輪中,把一條直線在一個圓上做純滾動,則這條直線上的一個定點的軌跡稱為齒輪的漸開線(即齒輪輪廓線),那么這個圓就叫齒輪的基圓。...
在定傳動比的齒輪傳動中,節點在齒輪運動平面的軌跡為一個圓,這個圓即為節圓。此時齒輪傳動可以認為兩個齒輪的節圓相切做純滾動。一對標準齒輪處在正確安裝位置時...
在齒輪的基圓圓周上,兩相鄰同一側面間的圓弧長為基圓齒距,也叫基節。用pb表示基圓齒距。...
中文名稱 基圓導程角 英文名稱 base lead angle 定義 (1)對於漸開線斜齒輪,指的是基圓螺旋線的導程角。(2)漸開線蝸桿的基圓螺旋線的導程角。 套用學科 ...
中文名稱 凸輪理論輪廓基圓 英文名稱 base circle of cam pitch curve;prime circle 定義 在盤形凸輪機構中,以凸輪軸心為圓心,凸輪理論輪廓最小向徑值為半徑...
中文名稱 凸輪工作輪廓基圓 英文名稱 base circle of cam contour 定義 在盤形凸輪機構中,以凸輪軸心為圓心、凸輪工作輪廓最小向徑值為半徑所作的圓。 套用...
中文名稱 漸開線蝸桿基圓 英文名稱 base circle of in-volute helicoid worm 定義 漸開線蝸桿基圓柱面與端平面的交線。 套用學科 機械工程(一級學科),傳動(...
廈門市景基圓商業資產流轉管理有限公司於2016年01月11日在廈門市湖裡區市場監督管理局登記成立。法定代表人申翌君,公司經營範圍包括對第一產業、第二產業、第三...
基圓隆突肩肖葉甲,體金屬藍黑色,部分淡紫至棕紅色;頭黑褐,腹面及後頭色較紅;觸角黑褐。主要分布於海南省。...
把一條沒有彈性的細繩繞在一個定圓上,拉開繩子的一端並拉直,使繩子與圓周始終相切。即在平面上,一條動直線(發生線)沿著一個固定的圓(基圓)作滾動的過程中,...
與一條曲線C的所有切線相交成直角的曲線Γ,稱為曲線C的漸開線(evolent)。一般的漸開線指“圓的漸開線”。在平面上,一條動直線(發生線)沿著一個固定的圓(基圓)...
一條直線在一個圓上作無滑動的滾動時,直線上一定點運動的軌跡稱為“圓的漸伸線”,而稱該圓為漸伸線的“基圓”,直線為漸伸線的“發生線”,如圖1(b)所示...
基圓上的周節叫基節,也就是基圓上的齒距。齒輪基節的具體含義,就是基圓齒距。舊稱基節。...
兩齒輪連心線上咬合接觸點各齒輪上留下軌跡稱為節圓,它的直徑就是節圓直徑。節圓直徑是齒輪參數中一個很重要的數字,齒輪上的很多數據都是與節圓直徑有關的,...
赤平極射投影網為等距離投影網,由基圓、經向大圓弧和緯向小圓弧的經緯線組成,標準的烏氏網其基圓直徑為20cm,經緯度間距為2°,用它能正確反映點、線、面的角...
雙曲型反演變換是反演變換的一種,指反演冪k>0的反演變換,這時k可表為k=r2(r>0),r稱為反演半徑,通常稱雙曲型反演變換為關於反演基圓(球)的反演變換。...
使透明紙上正北標記N與投影網正北重合,以N為0°,在基圓上順時針數至330°得一點A,為直線的傾伏向(圖7A)。把A點轉至東西直徑上(轉至南北直徑也可),由A...
