基本介紹
- 中文名:反射變換
- 外文名:reflection transformation
- 所屬學科:數學
- 簡介:歐氏幾何中一種重要變換
- 簡稱:反射
反射變換定義
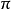
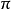
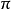
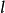
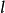
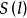
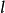
 圖1
圖1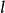
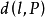
 圖2
圖2 圖2
圖2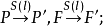
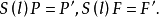
反射變換的主要性質
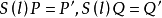

 圖3
圖3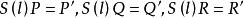
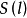
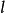
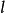
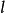
反射變換集合上的運算
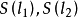
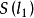

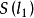

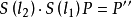
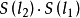
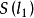

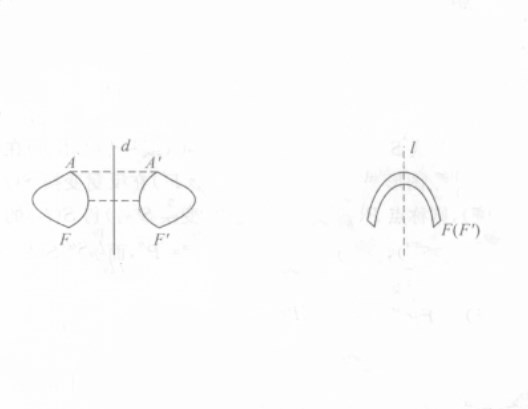
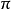
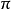
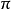
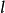
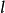
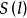
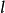
 圖1
圖1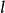
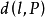
 圖2
圖2 圖2
圖2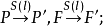
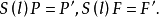
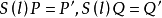

 圖3
圖3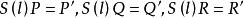
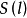
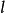
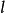
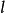
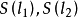
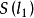

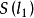

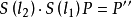
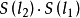
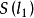

反射變換(reflection transformation)是歐氏幾何中一種重要變換,即歐氏平面上的軸反射變換和歐氏空間中的鏡面反射變換統稱反射變換,簡稱反射。...
鏡面反射變換(mirror reflection transformation)簡稱鏡面反射或平面反射,歐氏空間中的一種特殊變換。在歐氏空間中,把任一點A映成關於給定平面π對稱的點A′的變換稱...
若平面到自身的一一變換,使任意對應點的連結線段都通過某定點且被該點平方,則這個一一變換稱為點反射變換,簡稱點反射,定點稱為反射中心或對稱中心,對應點稱為關於...
中心反射變換(central reflection transformation)亦稱點反射,簡稱中心反射,是歐氏幾何中的一種重要變換。在歐氏平面或歐氏空間中,把任一點映成與一個給定的點S對稱...
空間旋轉反射(rotation reflection in space)是一種空間變換,如果f₁=ω(a,φ)是空間的一個旋轉角為φ的旋轉變換,a為旋轉軸,f₂是空間的一個面反射變換,...
坐標變換是空間實體的位置描述,是從一種坐標系統變換到另一種坐標系統的過程。通過建立兩個坐標系統之間一一對應關係來實現。是各種比例尺地圖測量和編繪中建立地圖...
本書從平面幾何對稱的知識出發,介紹反射變換的概念、性質和它在幾何極值問題、等周問題、光的傳播原理等方面的有趣套用;在此基礎上引出一般平面變換的概念,介紹平移...
初等幾何變換,是一個將幾何圖形按照某種法則或規律變成另一種幾何圖形的過程。它對於幾何學的研究有重要作用。初等幾何變換主要包括全等變換,相似變換,反演變換。...
《反射與反演》是2013-1出版的圖書,作者是嚴鎮軍。...... 《數林外傳系列·跟大學名師學中學數學:反射與反演(第2版)》從平面幾何對稱的知識出發,介紹反射變換的概...
