基本介紹 空間旋轉反射是指空間的旋轉反射變換,空間的
旋轉反射 與空間的面
反射變換 的乘積稱為空間的旋轉反射(變換),此變換屬於第二類契約變換。
空間旋轉變換是一種特殊的幾何變換,指空間的所有點繞同一直線旋轉同一角度的變換。旋轉變換簡稱旋轉,是歐氏幾何中的一種重要變換,即在歐氏平面上(歐氏空間中),讓每一點P繞一固定點(固定軸線)旋轉一個定角,變成另一點P′,如此產生的變換稱為平面上(空間中)的旋轉變換,此固定點(固定直線)稱為旋轉中心(旋轉軸),該定角稱為旋轉角。旋轉是第一種正交變換,在平面直角坐標系中,若旋轉中心為點M0 (x0 ,y0 ),點P(x,y)繞M0 旋轉定角θ後變成點P′(x′,y′),則平面上旋轉變換的代數表達式為
旋轉變換的逆變換也是旋轉變換,兩個繞同一點(同一軸線)的旋轉變換的乘積仍是旋轉變換,所有繞同一點(同一軸線)的旋轉變換的全體構成一個群,稱為旋轉群,在旋轉變換下,兩點間的距離與兩直線的交角均保持不變,旋轉變換的概念可以推廣到n維歐氏空間。繞O(0,0,…,0)點旋轉的代數表達式為
或用矩陣表示為:(x′
i )=(a
ij )·(x
i ),其中a
ij 為常數,且(x′
i ),(x
i )均為n×1矩陣,矩陣(a
ij )是行列式等於1的正交矩陣。
鏡面反射變換簡稱
鏡面反射 或平面反射,歐氏空間中的一種特殊變換。在歐氏空間中,把任一點A映成關於給定平面π對稱的點A′的變換稱為關於平面π的鏡面反射變換,平面π稱為反射平面。鏡面反射是第二種正交變換。在鏡面反射變換下,連結變換的每一對對應點A,A′所得到的線段都垂直於反射平面π且被π所平分,平面π上的點都是不動點,鏡面反射變換在直觀上相當於把平面π看做一面鏡子,變換前後的對應點就好比是物與像那樣,在空間直角坐標系中,若把坐標平面xOy取為反射平面,則鏡面反射變換的代數表達式為
其中(x,y,z),(x′,y′,z′)分別是變換前的點與變換後它的對應點的坐標。
相關介紹 如果一個圖形F在契約變換f下對應於圖形F',那么稱圖形F與F'契約。
我們不難發現,
契約變換 下,兩個對應圖形F與F'的邊界方向(順時針方向或逆時針方向)或者是一致的,或者是反向的。因此,按照對應圖形的邊
界方向可以將契約變換分為兩類:將使得對應圖形F與F'的邊界方向相同的契約變換稱為第一類契約變換(如圖1),而將使得兩個對應圖形F與F’邊界方向相反的契約變換稱為第二類契約變換(如圖2)。因而,我們將在第一類契約變換下的對應圖形F與F‘稱為
真正契約 ,而把第二類契約變換下的對應圖形F與F'稱為
鏡像契約 。
圖1 圖2 利用上述分類方式,我們容易得到,平移變換、旋轉變換(即兩個反射變換的乘積)是第一類契約變換,而反射變換是第二類契約變換。
既然平移變換、旋轉變換是兩個反射變換的乘積變換,那么(自然的思考),契約變換是否也是幾個反射變換的乘積變換呢?
我們猜測並可以證明:
性質1 任一契約變換至多可以表示為三個反射變換的乘積。
圖3 證明 設契約變換ω由三對不共線的對應點A與A',B與B',C與C'所確定(圖3)。
作AA’的垂直平分線
,那么,在以
為反射軸的反射變換下,△ABC變為△A'B
1 C
1 (若點A與A'重合,則沒有必要施行
)。此時,AB=A'B
1 =A'B'。
再作線段B
1 B'的垂直平分線
,則點A'必在
上,以
為反射軸的反射變換
將△A'B
1 C
1 變為△A'B'C
2 (如果B
1 與B'重合,也沒有必要施行變換
。此時A'C'=AC=A'C
1 =A'C
2 ,B'C'=BC=B
1 C
1 =B'C
2 。
最後作線段C'C
2 的垂直平分線
,點A'、B'必在直線
上。在反射變換
的作用下,△A'B'C
2 變為△A'B'C'(若點C'與C
2 重合,則不必施行變換
,於是,
綜上所述,對於第一類契約變換,總可以表示為兩個反射變換的乘積;對於第二類契約變換,總可以表示為一個反射變換或三個反射變換的乘積,於是得下表:
圖4 


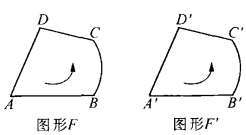 圖1
圖1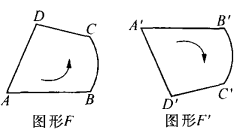 圖2
圖2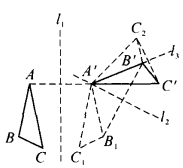 圖3
圖3













 圖4
圖4
