軸反射變換(axial reflection transformation)簡稱軸反射，是歐氏幾何中一種重要變換。在歐氏平面上或歐氏空間中，把任一點A映成關於給定直線S對稱的點A′的變換稱為關於直線S的軸反射變換，直線S稱為反射軸。平面軸反射是第二種正交變換，空間軸反射變換亦稱半周旋轉，它是旋轉角為π的空間繞反射軸的旋轉，因而是第一種正交變換。在軸反射變換下，連結每一對對應點A，A′所得到的線段都垂直於S，且被S所平分，反射軸上的每一點都是不動點，在平面直角坐標系中，若以x軸為反射軸，則軸反射的代數表達式為x'=x，y'=-y，其中(x，y)，(x′，y′)分別是變換前的點與它的對應點的坐標。
基本介紹
- 中文名：軸反射變換
- 外文名：axial reflection transformation
- 所屬學科：數學
- 所屬問題：高等幾何(仿射幾何)
- 簡稱：軸反射
基本介紹,相關定理,
基本介紹
設
是平面
的一條定直線，如果平面 的一個變換，使得對於平面 上不在直線 上的任意一點A與其對應點A’的連線AA'恆被直線 垂直平分，而直線l上的點都不動，則這個變換稱為平面 的軸反射變換，記作
。其中定直線 稱為反射軸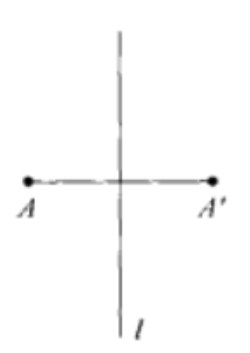(圖1)。
圖1按定義即知，反射軸上的點都是軸反射變換的不動點，且軸反射變換是可逆的，其逆變換就是自身。即
顯然，軸反射變換由反射軸唯一確定，也可由兩個非不動點的對應點唯一確定。
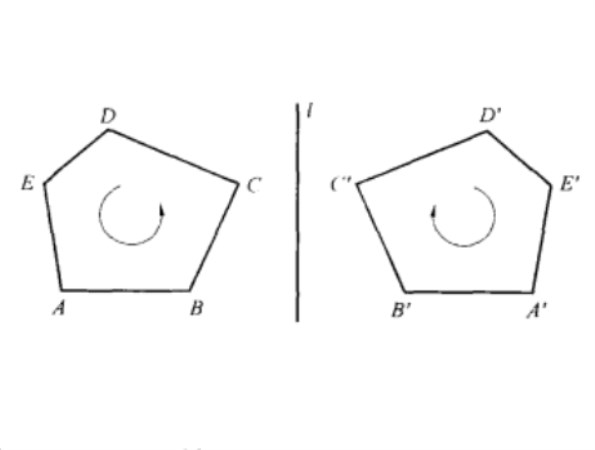
點A在軸反射變換 下的像A’也稱為圖形F關於直線l的對稱點；一個圖形F在軸反射變換 下的像F''則稱為圖形F關於直線l的對稱圖形，也稱圖形F與F'關於直線l對稱(圖2)。
圖2相關定理
定理1 軸反射變換是鏡像契約變換。
證明 設 是平面
的一個軸反射變換，對平面 上的任意兩點A、B，設
。
(1)如果A、B兩點都在反射軸f上(圖3)，則A’=A，B’=B，此時顯然有A’B’=AB。
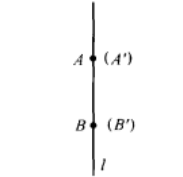圖3(2)如果A、B兩點中僅有一個點在反射軸l上，不妨設點A在l上(圖4)，則A’=A，由於A是線段BB’的垂直平分線l上的點，因此AB’=AB，即A’B’=AB。
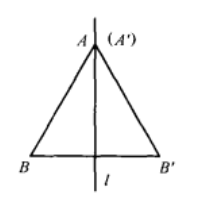圖4(3)如果4、B兩點都不在反射軸l上(圖5和圖6)，設線段AA’、BB'與l的交點分別為M、N，則M、N分別為線段AA’、BB’的中點，所以MA’=MA，MB'=MB，且
。於是，由
得
綜合(1)，(2)，(3)即知，S(l)是一個契約變換。
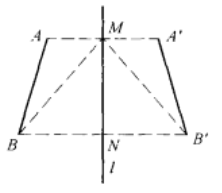圖5
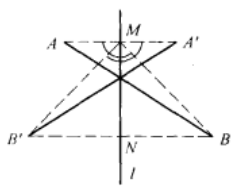圖6再設A、B是反射軸l上的兩個不同的點，而C是平面
上不在l上的一點(圖7)，則A、B是S(l)的兩個不動點。設
，則
與
是S(l)的兩個對應三角形，因l垂直平分線段CC’，所以C’、C分布在直線l的兩側，從而與異向。故S(l)是平面
的一個鏡像契約變換。
由相關定理知軸反射變換同樣具有契約變換的一切不變性質和不變數。
定理2 設S(l)是平面的一個軸反射變換，則
(1)點A是S(l)的不動點若且唯若A在反射軸l上；
(2)直線m是S(l)的不變直線若且唯若
或m與l重合。
證明 (1)由軸反射變換的定義即知。
(2)當或m與l重合時，由軸反射變換的定義即可知m是S(l)的不變直線。反之，設m是軸反射變換S(l)的一條不變直線。如果m上的每一個點都是S(l)的不動點，由(1)即知m與l重合，如果直線m上存在S(l)的一個非不動點，設
，則A’≠A。因m是S(l)的不變直線，所以A’也在直線m上，由軸反射變換的定義知，反射軸l垂直(平分)線段AA'，而A、A'是直線m上的兩個不同的點，故。
定理3 在軸反射變換下，任意一條非不變直線與其對應直線或相交於反射軸上，或皆與反射軸平行，並且反射軸上任意一點到兩對應直線的距離相等。
證明 設S(l)是平面的一個軸反射變換，平面上的直線m是S(l)的一條非不變直線，
，則m'≠m，若m與l相交於一點A(圖8)，因A在反射軸l上，所以A是S(l)的一個不動點，又A在直線m上，所以A也在其像直線m’上，即直線m'與m相交於反射軸l上的點A；若m∥l，而m’與反射軸l交於一點P，則由於m、m'互為像直線，所以直線m與l也交於P，這與m∥l矛盾，因此必有m'∥l(圖9)。
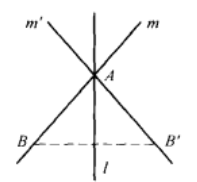圖8
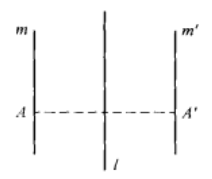圖9當m’與m相交於反射軸l上的一點A時(圖8)，在直線m上任取一點B，B≠A，並設
，則因l垂直平分線段BB'，所以l平分∠BAB’。從而反射軸l上的任意一點到直線m與m'的距離相等，當m’∥z∥m時(圖9)，在直線m上任取一點A，設
，則A’在直線m上，且
。因l垂直平分線段AA'，所以，l到直線m與m'的距離相等，即反射軸l上任意一點到直線m與m’的距離相等。
最後指出，軸反射變換作為一個契約變換，當然會保持兩直線的夾角大小不變，但軸反射變換是一個鏡像契約變換，因此它已經改變了角的方向，這個性質稱為軸反射變換的反向保角性。
三種契約變稱——平移變換、旋轉變換、軸反射變換是三種基本的契約變換，前兩種是真正契約變換，後一種是鏡像契約變換．這三種契約變換各有自己區別於其他契約變換的一些獨特的性質，這三種契約變換基本上窮盡了平面上的所有契約變換。
