基本介紹
- 中文名:對稱變換
- 外文名:symmetrical transformation
- 相關術語:反對稱變換
- 學科:數學
- 套用:數形結合處理、圖像處理
- 基本概念:在某一作用下仍與原來的圖形重合
形狀對稱變換
合成
性質
分類
逆變換
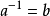



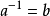


若一個平面圖形K在平面剛體運動m的作用下仍與原來的圖形重合,就說K具有對稱性,m叫做K的對稱變換。對稱變換一般分為:關於X軸或Y軸對稱、關於某一點對稱、關於某...
由一個平面圖形變為另一個平面圖形,並使這兩個圖形關於某一條直線成軸對稱,這樣的圖形改變叫做圖形的軸對稱變換,也叫做反射變換,簡稱反射(reflection)。...
對稱性變換是指在描述任何物體(幾何圖形、晶體、函式)的變數空間時都可以對它的整體作適當的變換,如果這種變換使物體本身重合(即它在變換後不變亦即轉換成自身),...
對稱原理亦可以解讀為對稱效應,即在沒有關聯的2個領域中,如果有一個事物能夠同時存在於這2個領域,那么我們就可以將這個事物看做一個對稱軸線,並且基於這個軸線,...
非點式對稱變換是指晶體內部結構是無限多個結構基元在三維空間中不連續地間斷地周期地分布的,即在晶體內的物質點是不連續地間斷地周期地分布的。這樣就需要描述...
對稱矩陣(Symmetric Matrices)是指以主對角線為對稱軸,各元素對應相等的矩陣。線上性代數中,對稱矩陣是一個方形矩陣,其轉置矩陣和自身相等。1855年,埃米特(C....
數學裡的圖象變換,指一個圖形(或表達式)到另一個圖形(或表達式)的演變。圖象變換是函式的一種作圖方法。已知一個函式的圖象,通過某種或多種連續方式變換,得到另...
對稱性是物質的狀態和運動規律在對稱變換下的性質。它已成為物理學中一個最普遍而深刻的觀念。對稱性和守恆定律有著深刻的聯繫。對稱性反映的是客觀物質世界結構...
《對稱性原理》唐有祺著,科學出版社1977年出版。對稱性所涉及的原子空間分布問題,是化學科學中的一個基本問題。...
滿足量子化要求的協變規範下的QCD拉氏量,由於存在規範固定項和鬼場項而丟失了定域規範不變性。即拉氏量在通常的無窮小規範變換下不是不變的, QCD拉氏量在BRST...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
使幾何圖形成軸對稱或旋轉對稱的直線。對稱圖形的一部分繞它旋轉一定的角度後,就與另一部分重合。 許多圖形都有對稱軸。例如橢圓、雙曲線有兩條對稱軸,拋物線有一...
在魔方最少步驟還原中,若某狀態可由某一還原態經一系列操作X1X2...Xn達到,則稱以下兩類狀態為當前狀態的對稱態:取任意一還原態,執行X1X2...Xn並在之前及...
近代物理學中的重要觀念。如果運動規律具有一種對稱性,必相應地存在一條守恆定律。...... 例如物理規律具有空間平移變換對稱性,表明空間沒有絕對的原點,可以任意選擇...
