富克斯變換

簡介

分式線性變換是一種特殊的映射。從擴充z平面到擴充w平面到共形映射稱為分式線性變換，簡稱線性變換，即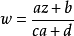

，其中a，b，c，d都是復常數，ad-bc≠0並且當z=∞時對應w=a/c，z=-d/c時對應w=∞。

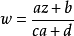
分式線性變換總可以分解成下述簡單類型變換的複合：

1、w=kz+h(k≠0)；

2、w=1/z；

a，b，c，d都是實數且滿足ad-bc>0的分式線性變換稱為富克斯變換。

富克斯變換將上半平面映為上半平面，使Ox軸(z=x+iy)上各點z與Ou軸(w=u+iv)上各點w對應。

彭加勒在論文《數學上的發現》中記敘了他的靈感思維過程。1880年他研究富克斯的變換方法，其靈感也產生於思維放鬆的時候，“我的腳剛踏上剎車板．突然想到一種構想……，我用定義富克斯函式的變換方法同非歐幾何的變換方法是完全一樣的”。

彭加勒研究富克斯函式經歷了很長的時間、其中包括他在服兵役期間也一直研究。