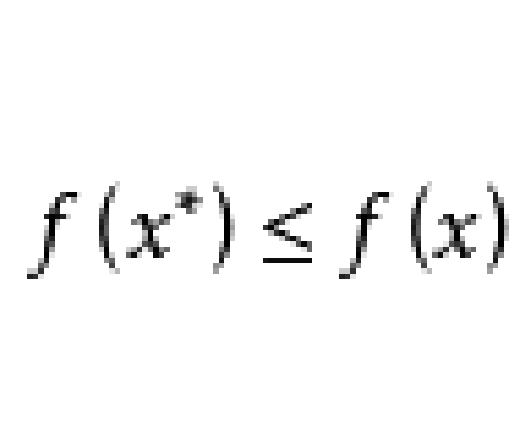全局極小點(global minimum point)是在可行域X⊂R上使目標函式f(x)達到極小值的點,即:
1.設f是定義在開凸集X⊂R上的連續擬凸函式,且在x*∈X處可微,▽f(x*)=0,則x*是f(x)在X上的全局極小點的充分必要條件是:對任意的x∈X,恆有▽f(x*)(x-x*)≥0;
2.設f是開凸集X⊂R上的偽凸函式,又設對某個點x*∈X有▽f(x*)=0,則x*是f(x)在X上的全局極小點;
3.設f是凸集X⊂R上的嚴格擬凸函式,x*∈X是f(x)在X上的局部極小點,則x*必為f(x)在X上的全局極小點;
4.設f是凸集X上的擬凸函式,若x*是f(x)在X上的一個嚴格局部極小點,則x*也是f(x)在X上的嚴格全局極小點。
基本介紹
- 中文名:全局極小點
- 外文名:global minimum point
- 所屬學科:數學
- 所屬問題:運籌學(非線性規劃)
- 相關概念:凸函式,極小值,目標函式等
基本介紹















全局極值














凸函式的全局極小點