突變約定

突變約定(catastrophe convention)是突變理論的一個基本概念，是用來確定在兩個或多個平衡位置中的選擇準則。設f：M×U→R為一突變模型的勢函式，在點u∈U的一個局部系是f|M×{u}→R的一個局部極小點，一個過程是一個可微映射s：U′→M，滿足s(u)是一個局部系或-∞，u∈U′，U′是U的開稠密集，一個突變約定是指定一個過程於勢函式f，最基本的約定有兩種：麥克斯韋約定和完全延遲約定。

基本介紹

• 中文名：突變約定
• 外文名：catastrophe convention
• 所屬學科：數學（突變理論）
• 簡介：確定在多個平衡位置中的選擇準則

基本介紹

突變理論適用於梯度系統，但這時該系統需處於靜態或準靜態，沒有考慮到動力學效應和漲落(系統的狀態在平衡位置附近的微小變動)的影響。於是嚴格來說，根本就不可能實現從一個平衡位置到另一個平衡位置的轉換，因為要進行轉換需要某種形式的運動。因此，我們要約定這種轉換在一定的條件下是可能產生的，並且約定轉換進行的方式。

值得指出的是，雖然一個經典的確定性系統(例如勢能為的一維諧振子)可以用勢的極小點完整地描述，但是一個量子力學諧振子的狀態卻需要用一個中心點在a的機率分布來描述，這個分布的寬度取決於Schrodinger方程中擴散項的係數。對於這類系統，必須注意漲落水平與勢壘高度的相對大小。

考慮用勢函式描寫的系統，這個系統原來處於勢函式的一個全局極小點，當參數t變化時，勢函式的形狀會有所變動，原來的全局極小點可能轉化為一個局部極小點而不再是全局極小點，也可能消失。我們需要作某種約定來確定系統在新的勢函式下所處的位置，最常用的約定有兩種：

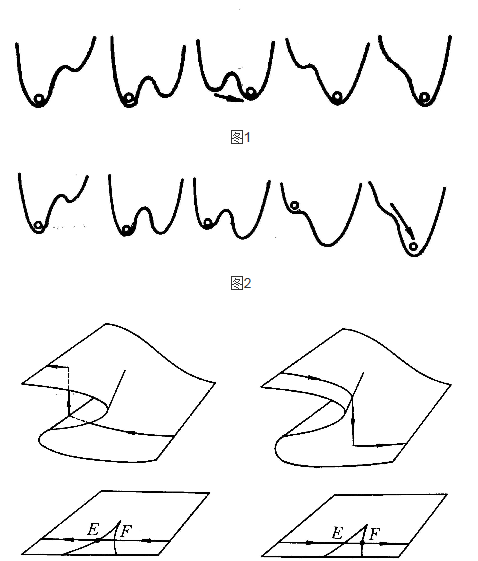
(1)Maxwell約定。系統總是轉移到使它的勢全局極小的穩定平衡位置。對於參數空間U中的u，當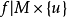有兩個以上的穩定極小值時，s(u)總是選取絕對極小值(即極小值中之最小者)，因此，突變僅出現在勢函式有兩個以上的絕對極小值時(如圖1)。

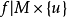
圖1

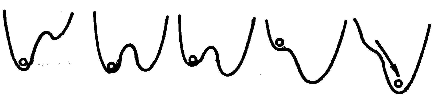圖2

(2)理想延遲約定。也稱完全延遲約定，系統留在原來的穩定平衡位置上，直到這個穩定平衡位置消失。當控制參數u在U中變化時，過程s(u)總是儘可能久地連續延伸，直到“無路可走”時為止(如圖2)，此時穩定的平衡狀態消失在一個退化的臨界點，從而使得勢f_u有退化臨界點的u的軌跡起著重要的作用，在齊曼突變機械中，當自由端P在(u，v)平面上移動，從尖點形區域的右方進入而從左方穿出時(如圖3)，在點E處(而不是在點F)引起狀態曲面M上相應軌跡的跳躍，自由端P移動的軌跡反向移動，從尖點形的左方穿入，從右方穿出(如圖4)，相應的M上的過程軌跡不在點E而是在點F處引起突變，這便是“使過程儘可能連續保持”的原則。

圖3

圖4

不同突變約定的選用

對於梯度動力學系統

當所有的時，採用理想延遲約定比較合理，因為位勢變化緩慢，系統無從得知其他極小點的情況。但是對於用分布函式描述的系統，它是否趨於全局極小點。則取決於勢壘高度與漲落水平N的相對大小。當時。應採用理想延遲約定，而當時，應採用Maxwell約定(圖5)。因此，這兩種約定可以被看作兩種極限情況。

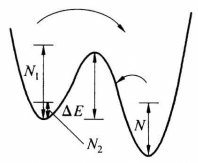圖5不同約定的選用

：理想延遲約定；：Maxwell約定。

採用不同約定時的分叉集當然也不相同，採用理想延遲約定時的分叉集取決於這個局部條件，稱為局部分叉集，如我們前面所討論的。而採用Maxwell約定時的分叉集由Clausius-Clapeyron方程確定，稱為非局部分叉集。圖6示出了對尖點突變的兩種分叉集，以及參數變化時系統狀態的軌跡。其中D(d)記理想延遲約定，M(m)記Maxwell約定。但實際情況也可能介於這兩種極限狀況之間，這時分叉集是一個模糊集。

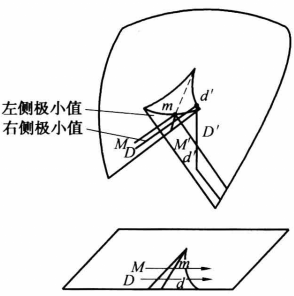圖6兩種約定下的分叉集和系統狀態變化軌跡

這兩種約定都沒有考慮動力學效應，下面的例子說明了動力學效應的影響。考慮阻尼振子

其中，並且

設V(x)的圖形如圖7所示，原來有三個穩定平衡位置，系統處於左面的穩定平衡位置。當參數變化時，這個平衡位置消失，根據理想延遲約定，系統將進入另一個穩定平衡位置。但究竟是哪一項呢?如果採用

那么可以認為系統將靜止在中間的平衡位置()上，因為這裡速度為零。但對於式(2)控制的系統，其最終位置實際上取決於γ值的大小和各穩定平衡位置的分布情況。這個問題可以通過對吸引域的形狀考慮來加以解決，圖3中給出了只考慮γ變化時的示意定性結果，γ越小，交替越頻繁。

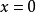
在突變理論的大多數套用中都選用理想延遲約定，並且不考慮動力學效應。

圖7 阻尼振子的最終狀態與阻尼係數之間的關係