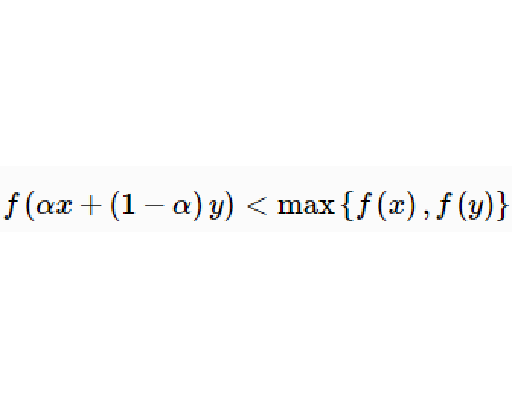嚴格擬凸函式

嚴格擬凸函式(strictly quasi-convex function)是凸集上的一類函式。設S是線性空間中的非空凸集，f是S上的實值函式。若對任何實數α∈(0，1)和任意的x，x∈S，且f(x)≠f(x)，恆有f(αx+(1-α)x)<max{f(x)，f(x)}，則稱f是S上的嚴格擬凸函式，或f在S上是嚴格擬凸的。

基本介紹

• 中文名：嚴格擬凸函式
• 外文名：strictly quasi-convex function
• 所屬問題：運籌學(非線性規劃)
• 相關概念：凸函式、擬凸函式等

定義

下面一系列定義中的函式都是定義在n維歐氏空間中的某一凸集合上的n個變數的實值函式。

定義1 若對於任意的，以及數，有

則稱是上的嚴格凸函式。

定義2 若對於任意的，以及數，有

則稱是上的凸函式。

定義3若對於任意的以及數，有

則稱是上的嚴格擬凸函式。

定義4若對於任意的，及數，有

則稱是上的擬凸函式。

定義5 若對於任意的，以及數，有

則稱是上的下單峰章捆櫻灑函式(或稱直線單峰函式)。

當時，下單峰函式的定義與優選法中單變數的單峰函式的定義是一致的。因此，定義5是單變數單峰函式的形式上的擴充。

定義6 設是一個非空凸集，並設。如果對每對，都有

則稱為強擬凸。若為強擬凸，則便稱為一個強擬凹函式。

相關性質

不符狼難看出定義中所述的函式類之間有如下的關係：記民符

嚴格凸函式凸函式嚴格擬凸函式；

嚴格凸函式下單峰函式；

下單峰函式嚴格擬凸函式。

(“”的意思是：例如“嚴格凸函式凸函式”是表示若是上的嚴格凸函式，則也是上的凸函式)。當在上是下半連續函式時，可以證明下面的關係成立：

嚴格擬凸函式擬凸函式；

不難證明，當是上的嚴格擬凸函龍斷榜數時，局部極小也是整體極小( 最優解)；當是上的下單樂采船峰函式時，其最優解( 若存在) 唯一。

不難證明，是上面定義1至定義5中的某一函式類中n個變數的函式的充分必要條件是：對任意的，單變數函式

是上的同類型的函式類中的單變數的函式。

下面這條定理指出：在整個凸集上，嚴格擬凸函式的局部極小值也是一個總體極小值。但是從圖1(a)中可以看到，擬凸函式就沒有這種特性。

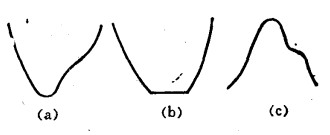圖1 嚴格擬凸函式和嚴格擬凹函式

(a)嚴格擬凸；(b)嚴格擬凸；(c)嚴格擬凹

定理1 設為嚴格擬凸。考慮下述規劃問題(P)：

這裡一個非空凸集。如果是一個局部最優解，則也禁愚漏是一個總體最優解。

引理2設是一個非朵影夜捆空凸集，並設為嚴格擬凸和下半連續，則是一個擬凸函式。

下面說法均成立：

①每個嚴格凸函式都是強擬凸函式。

②每個強擬凸函式都是嚴格擬凸函式。

⑨每個強擬凸函式都是擬凸函式，即使沒有半連續的假定也是如此。

定理3 設為強擬凸函式。考慮下面的規劃問題(P)：

這裡是一個非空凸集。若是一個局部最優解，則便是唯一的總體最優解。