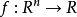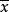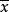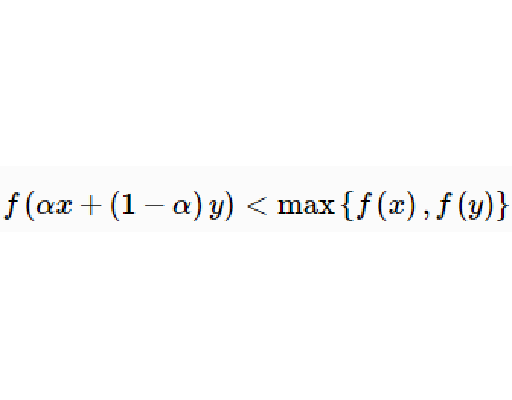嚴格擬凸函式(strictly quasi-convex function)是凸集上的一類函式。設S是線性空間中的非空凸集,f是S上的實值函式。若對任何實數α∈(0,1)和任意的x1,x2∈S,且f(x1)≠f(x2),恆有f(αx1+(1-α)x2)<max{f(x1),f(x2)},則稱f是S上的嚴格擬凸函式,或f在S上是嚴格擬凸的。
基本介紹
- 中文名:嚴格擬凸函式
- 外文名:strictly quasi-convex function
- 所屬問題:運籌學(非線性規劃)
- 相關概念:凸函式、擬凸函式等
定義,相關性質,
定義
下面一系列定義中的函式 都是定義在n維歐氏空間
都是定義在n維歐氏空間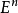 中的某一凸集合
中的某一凸集合 上的n個變數的實值函式。
上的n個變數的實值函式。

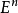

定義1 若對於任意的 ,以及數
,以及數 ,有
,有




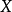
定義2 若對於任意的 ,以及數
,以及數 ,有
,有


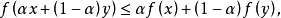

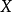
定義3若對於任意的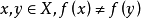 以及數
以及數 ,有
,有
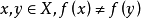




定義4若對於任意的 ,及數
,及數 ,有
,有





定義5 若對於任意的 ,以及數
,以及數 ,有
,有



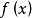

當 時,下單峰函式的定義與優選法中單變數的單峰函式的定義是一致的。因此,定義5是單變數單峰函式的形式上的擴充。
時,下單峰函式的定義與優選法中單變數的單峰函式的定義是一致的。因此,定義5是單變數單峰函式的形式上的擴充。

定義6 設 是一個非空凸集,並設
是一個非空凸集,並設 。如果對每對
。如果對每對 ,都有
,都有




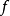

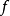
相關性質
不難看出定義中所述的函式類之間有如下的關係:
嚴格凸函式 凸函式
凸函式 嚴格擬凸函式;
嚴格擬凸函式;


嚴格凸函式 下單峰函式;
下單峰函式;

下單峰函式 嚴格擬凸函式。
嚴格擬凸函式。

(“ ”的意思是:例如“嚴格凸函式
”的意思是:例如“嚴格凸函式 凸函式”是表示若
凸函式”是表示若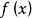 是
是 上的嚴格凸函式,則
上的嚴格凸函式,則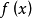 也是
也是 上的凸函式)。當
上的凸函式)。當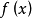 在
在 上是下半連續函式時,可以證明下面的關係成立:
上是下半連續函式時,可以證明下面的關係成立:


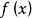

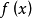

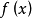

嚴格擬凸函式 擬凸函式;
擬凸函式;

不難證明,當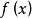 是
是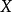 上的嚴格擬凸函式時,局部極小也是整體極小( 最優解);當
上的嚴格擬凸函式時,局部極小也是整體極小( 最優解);當 是
是 上的下單峰函式時,其最優解( 若存在) 唯一。
上的下單峰函式時,其最優解( 若存在) 唯一。
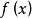
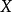


不難證明, 是上面定義1至定義5中的某一函式類中n個變數的函式的充分必要條件是:對任意的
是上面定義1至定義5中的某一函式類中n個變數的函式的充分必要條件是:對任意的 ,單變數函式
,單變數函式





下面這條定理指出:在整個凸集上,嚴格擬凸函式的局部極小值也是一個總體極小值。但是從圖1(a)中可以看到,擬凸函式就沒有這種特性。
 圖1 嚴格擬凸函式和嚴格擬凹函式
圖1 嚴格擬凸函式和嚴格擬凹函式(a)嚴格擬凸;(b)嚴格擬凸;(c)嚴格擬凹
定理1 設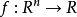 為嚴格擬凸。考慮下述規劃問題(P):
為嚴格擬凸。考慮下述規劃問題(P):
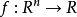
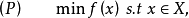
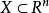
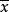
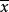
引理2設 是一個非空凸集,並設
是一個非空凸集,並設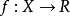 為嚴格擬凸和下半連續,則
為嚴格擬凸和下半連續,則 是一個擬凸函式。
是一個擬凸函式。

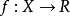

下面說法均成立:
①每個嚴格凸函式都是強擬凸函式。
②每個強擬凸函式都是嚴格擬凸函式。
⑨每個強擬凸函式都是擬凸函式,即使沒有半連續的假定也是如此。
定理3 設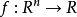 為強擬凸函式。考慮下面的規劃問題(P):
為強擬凸函式。考慮下面的規劃問題(P):