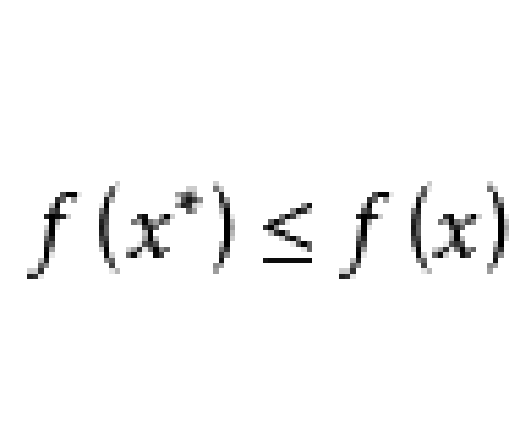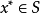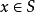全局極小點(global minimum point)是在可行域X⊂Rn上使目標函式f(x)達到極小值的點,即:
1.設f是定義在開凸集X⊂Rn上的連續擬凸函式,且在x*∈X處可微,▽f(x*)T=0,則x*是f(x)在X上的全局極小點的充分必要條件是:對任意的x∈X,恆有▽f(x*)T(x-x*)≥0;
2.設f是開凸集X⊂Rn上的偽凸函式,又設對某個點x*∈X有▽f(x*)=0,則x*是f(x)在X上的全局極小點;
3.設f是凸集X⊂Rn上的嚴格擬凸函式,x*∈X是f(x)在X上的局部極小點,則x*必為f(x)在X上的全局極小點;
4.設f是凸集X上的擬凸函式,若x*是f(x)在X上的一個嚴格局部極小點,則x*也是f(x)在X上的嚴格全局極小點。
基本介紹
- 中文名:全局極小點
- 外文名:global minimum point
- 所屬學科:數學
- 所屬問題:運籌學(非線性規劃)
- 相關概念:凸函式,極小值,目標函式等
基本介紹,全局極值,凸函式的全局極小點,
基本介紹
定義1 若對於任意的 ,都有
,都有

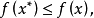
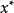
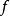
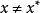
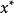
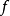
定義2 若對於任意的 ,都有
,都有

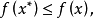

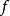
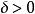
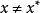
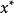
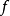
由上述定義可知,全局極小點一定是局部極小點,反之不然.一般來說,求全局極小點是相當困難的,因此,通常只求局部極小點(在實際套用中,有時求局部極小點已滿足了問題的要求)。
全局極值
全局極值(global extreme value)是實值函式在某區域取得極小或極大的值。設X為R中的集合,f為X上的實值函式,對於 ,如果對所有的
,如果對所有的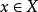 均滿足
均滿足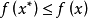 (
(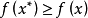 ),則稱
),則稱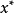 為
為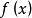 在X上的全局極小(大)點,
在X上的全局極小(大)點,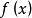 為全局極小(大)值。若對所有的
為全局極小(大)值。若對所有的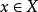 ,且
,且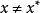 ,均有
,均有 (
( ),則稱
),則稱 為
為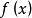 在X上的嚴格全局極小(大)點,
在X上的嚴格全局極小(大)點,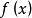 為嚴格全局極小(大)值。
為嚴格全局極小(大)值。

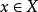
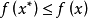
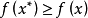
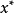
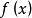
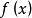
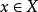
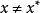



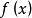
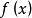
凸函式的全局極小點
1.若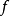 為定義在凸集S上的凸函式,則它的任一局部極小點就是它在S上的全局極小點,而且它的極小點形成一個凸集。
為定義在凸集S上的凸函式,則它的任一局部極小點就是它在S上的全局極小點,而且它的極小點形成一個凸集。
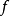
3.定義在凸集上的凸函式的駐點(梯度為0的點),就是其全局極小點。全局極小點並不是惟一的,但若為嚴格凸函式,則其全局極小點是惟一的。