基本介紹
- 中文名：二次規劃
- 外文名：quadratic programming
- 定義：一類特殊數學規劃問題
- 類型：組合最佳化科學的基本方法
- 解法：Lemke方法、內點法
- 學科：數學
一般形式,解法,有效集法求解一般凸二次規劃問題,理論基礎,算法步驟,拉格朗日方法求解等式約束二次規劃問題,
一般形式
二次規劃的一般形式可以表示為：
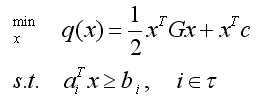二次規劃一般形式其中G是Hessian矩陣，τ是有限指標集，c，x和
，都是R中的向量。如果Hessian矩陣是半正定的，則我們說該式是一個凸二次規劃，在這種情況下該問題的困難程度類似於線性規劃。如果有至少一個向量滿足約束並且在可行域有下界，則凸二次規劃問題就有一個全局最小值。如果是正定的，則這類二次規劃為嚴格的凸二次規劃，那么全局最小值就是唯一的。如果是一個不定矩陣，則為非凸二次規劃，這類二次規劃更有挑戰性，因為它們有多個平穩點和局部極小值點。
解法
已經出現了很多求解二次規劃問題的算法，如拉格朗日方法、Lemke方法、內點法、有效集法、橢球算法等等，並且仍有很多學者在從事這方面的研究工作。
在數學規劃中，由於凸二次規劃有著特殊作用，人們一直把它作為一個重要課題加以研究。等式約束二次規劃問題的一個求解方法是拉格朗日算法。首先定義拉格朗日函式，對此函式求導，再令導數為零，這樣便得到一個線性方程組。拉格朗日算法有兩個不足之處：
（1）構造的線性方程組的方程個數與m有關(n+m個方程)，當n與m都很大時，將占用計算機很大的存儲空間，並且使計算量增加；
（2）必須計算矩陣的逆。
有效集法求解一般凸二次規劃問題
理論基礎
首先引入下面的定理，它是有效集方法理論基礎。
設x*是一般凸二次規劃問題的全局極小點，且在x*處的有效集為
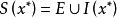
則x*也是下列等式約束凸二次規劃：
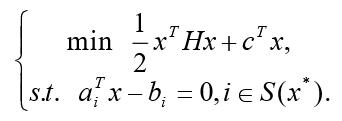
的全局最小點。
從上述定理可以發現，有效集方法的最大難點是事先一般不知道有效集S(x*)，因此只有想辦法構造一個集合序列去逼近它，即從初始點
出發，計算有效集
，解對應的等式約束子問題。
修正後的子問題如下：
由此可知，修正後的子問題的全局極小點必然是原問題的一個下降可行方向。
算法步驟
有效集方法的算法步驟如下：
（1）選取初值。給定初始可行點 ，令k:=0。
（2）解子問題。確定相應的有效集
求解子問題
得極小點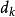
和拉格朗日乘子向量
。若
轉步驟（4）；否則，轉步驟（3）。
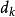
（3）檢驗終止準則。計算拉格朗日乘子：
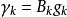
其中
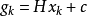
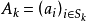
令
若
，則
是全局極小點，停算；否則，轉步驟（2）。
（4）確定步長
。令
，其中
令
。
（5）若 =1，則令
；否則，若 <1，則令
，其中
（6）令k:=k+1，轉步驟（1）。
拉格朗日方法求解等式約束二次規劃問題
我們考慮如下的二次規劃問題：
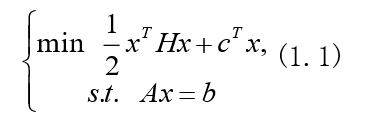
其中矩陣H對稱正定，A行滿秩。
首先寫出拉格朗日函式：
令
將上述方程組寫成分塊矩陣形式：
我們稱此方程組的係數矩陣：
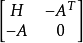
為拉格朗日矩陣。
解的表達式為：
