么半群,是指在抽象代數此一數學分支中,么半群是指一個帶有可結合二元運算和單位元的代數結構。
么半群在許多的數學分支中都會出現。在幾何學中,么半群捉取了函式複合的概念。
結合的酉群胚叫么半群。例如,賦以加法(或乘法)的自然數集N是么半群。
基本介紹
- 中文名:么半群
- 外文名:monoid group
- 領域:數學
- 學科:抽象代數
- 性質:代數結構
- 定義:結合的酉群胚
定義


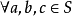


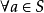
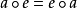
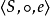
半群
衍生概念
交換么半群
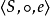

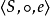
冪關係
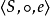
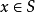
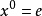


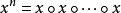
子么半群
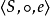
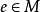

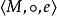
自然預序
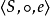

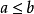


序單位


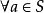

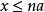

么半群,是指在抽象代數此一數學分支中,么半群是指一個帶有可結合二元運算和單位元的代數結構。
么半群在許多的數學分支中都會出現。在幾何學中,么半群捉取了函式複合的概念。
結合的酉群胚叫么半群。例如,賦以加法(或乘法)的自然數集N是么半群。


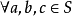


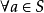
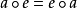
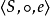
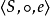

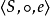
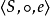
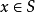
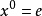


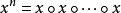
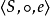
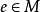

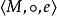
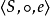

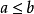




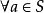

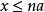
么半群,是指在抽象代數此一數學分支中,么半群是指一個帶有可結合二元運算和單位元的代數結構。么半群在許多的數學分支中都會出現。在幾何學中,么半群捉取了...
半群是一個二元運算的代數系統。半群的正式研究開始於二十世紀早期。自從1950年代,有限半群的研究在理論計算機科學中變得特別重要,因為在有限半群和有限自動機之間...
語法么半群,即在數學中,形式語言 L 的 語法么半群 M(L) 是可識別語言 L 的最小的么半群。...
偏序么半群(po-monoid)亦稱偏序近群一種特殊的半群.具有單位元1(即對任意、,x1一1、一x)的偏序半群稱為偏序么半群.任意偏序群都是偏序么半群. ...
可除么半群(divisibility monoid)亦稱可除近群一類重要的偏序么半群.設M是偏序么半群,若a鎮b等價於b E Ma及bEaM,則稱偏序么半群M為可除么半群.赫爾德(...
《么半群理論的同調方法》是科學出版社出版的圖書。本書提供了一個么半群的地區綜合調查。它包括內射和弱內射系,投射S-系的概念,對強度的一些基本的和有趣的...
備格序么半群(complete lattice-ordered mon-oid)亦稱c1么半群.一類重要的格序么半群.設M是具有二元乘法運算的備格,若乘法對並滿足無限分配律: 則稱M為備格...
諾特格序么半群(Noetherian lattice-orderedmonoid )一類重要的格序么半群.若格序么半群L是整的、交換的,且作為格滿足升鏈條件,則稱L為諾特格序么半群.沃德(...
實格序子么半群(solid lattice-ordered sub-monoid)一類具有特殊性質的格子么半群.設A是格序半群,且是S的格序子么半群.若A的正錐A+是S+的m理想,則A稱...
戴德金格序么半群(Dedekind lattice-orderedmonoid )一類重要的格序么半群.設L是交換的剩餘格序么半群,若1.的負錐滿足升鏈條件,則稱L為戴德金格序么半群....
《半群的S系理論》是1999年科學出版社出版的圖書,作者是劉仲奎、喬虎生。...... 主要內容包括:半群S-系理論的基本概念、投射性、內射性、平坦性、平坦性對么半...
稱從E到F中的映射f是群胚同態,如果對於E的任一元素偶(x,y),有:設E與F為兩個么半群(兩個群),稱從E到F中的映射。f是么半群(群)的同態,如果f是群胚...
稱從E到F中的映射f是群胚同態,如果對於E的任一元素偶(x,y),有設E與F為兩個么半群(兩個群),稱從E到F中的映射。f是么半群(群)的同態,如果f是群胚...
(在群的情況下,後一個條件是自然滿足的,但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態, 而並不因此就是么半群的同態)。設G為乘法群,而a為G...
稱從E到F中的映射f是群胚同態,如果對於E的任一元素偶(x,y),有:[1] 設E與F為兩個么半群(兩個群),稱從E到F中的映射。f是么半群(群)的同態,如果f...
設E與F為兩個群胚,兩個么半群,兩個群,兩個環,兩個向量空間,兩個代數或兩個酉代數。稱從E到F中的映射f是同構,如果f有逆映射,並且f與f-1是兩個同態。...
例子包括么半群乘法選取為合取的布爾代數,在串接運算之下的給定字母表 Σ 的所有形式語言的集合,在關係複合運算之下的給定集合X上所有二元關係的集合,和更一般的...
的態射恰好是么半群的元素,且其態射複合由么半群的運算所給定。么半群令態射絕不可能為函式,唯一從單元素集合x至x的函式為當然函式。可視範疇為廣義化了的麼...
獨立完成的研究論文“圖的組合結構和圖的自同態么半群的代數結構”獲廣東省自然科學優秀論文三等獎(1999年),研究成果“圖及其自同態么半群”獲國務院僑辦科技進步...
擬群-除法總是可能的非空原群; 環群-有單位元的擬群; 半群-運算為可結合的原群; 么半群-有單位元的半群; 群-有逆元的么半群,或等價地說,可結合的環...
f是么半群(群)的同態,如果f是群胚的同態,且E的中性元素的象是F的中性元素. (在群的情況下,後一個條件是自然滿足的,但是從加法么半群N到乘法么半群N的...
此么半群服從消去律,可嵌入一群內:最小的是整數群。 同理,乘法運算“×”定義為: a× 0 = 0; a× S(b) = a × b + a (N,×)亦是交換么半群...
的函式所組成之么半群的單位元。,因為么半群的單位元是唯一的,可以以 上的單位元來替代其恆等函式的定義。此一定義廣義化成了於範疇論中恆等態射的概念,其中 ...
