基本介紹
- 中文名:同餘類
- 外文名:congruence class或residue class
- 領域:數學
同餘符號,同餘類,餘數系統,性質,整除性,傳遞性,保持基本運算,除法原理,同餘關係式,威爾遜定理,費馬小定理,歐拉定理,卡麥可函式,階乘冪,套用,
同餘符號
記作

讀作 同餘於
同餘於 模
模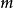 ,或讀作
,或讀作 與
與 關於模
關於模 同餘。
同餘。


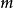



比如 。
。

同餘於的符號是同餘相等符號≡。統一碼值為 U+2261。但因為方便理由,人們有時會把它(誤)寫為普通等號 (=)。
同餘類
如同任何同餘關係,對於模 同餘是一種等價關係,整數
同餘是一種等價關係,整數 的等價類是一個集合
的等價類是一個集合 ,標記為
,標記為 。由對於模
。由對於模 同餘的所有整數組成的這個集合稱為同餘類(congruence class或residue class);假若從上下文知道模
同餘的所有整數組成的這個集合稱為同餘類(congruence class或residue class);假若從上下文知道模 ,則也可標記為
,則也可標記為 。
。







同餘類中的每個元素都可以拿來代表該同餘類,稱為該同餘類的代表數(英語:representative)。
餘數系統
餘數系統(英語:residue system)亦即模n同餘類的代表數的集合,通常使用的代表數是最小非負整數,因為它是除法中的應當餘數。要注意的是,對於同一個模數n,不同的同餘類不等價,亦即,屬於不同同餘類的整數不同餘於模數n,或者說,模n餘數系統中的任二元素不同餘於模n;而且,整數域中的每個整數隻屬於模數n的一個同餘類,因為模n將整數域劃分為互斥區塊,每個區塊是一個同餘類。
一個完整餘數系統(英語:complete residue system)指的是模n的全部同餘類的代表數的集合;因為餘數系統中的任二元素不同餘於模n,所以它也稱為非同餘餘數的完整系統(英語:complete system of incongruent residues)。例如,模3有三個同餘類 ,其完整餘數系統可以是
,其完整餘數系統可以是 。如果該集合是由每個同餘類的最小非負整數所組成,亦即
。如果該集合是由每個同餘類的最小非負整數所組成,亦即 ,則稱該集合為模n的最小餘數系統(英語:least residue system)。
,則稱該集合為模n的最小餘數系統(英語:least residue system)。



模n完整餘數系統中,與模n互質的代表數所構成的集合,稱為模n的簡約餘數系統(英語:reduced residue system),其元素個數記為 ,亦即歐拉函式。例如,模
,亦即歐拉函式。例如,模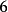 的簡約餘數系統為
的簡約餘數系統為 或
或 。如果模n是質數,那么它的最小簡約餘數系統是
。如果模n是質數,那么它的最小簡約餘數系統是 ,只比最小餘數系統少一個0。
,只比最小餘數系統少一個0。




性質
整除性
(即是說 a 和 b 之差是 m 的倍數)
換句話說,
換句話說,

同餘可以用來檢驗一個數是否可以整除另外一個數,見整除規則。
傳遞性

保持基本運算


除法原理
同餘關係式
威爾遜定理

費馬小定理