在數學中,傅立葉級數是一種三角級數,傅立葉級數也常稱為三角級數。但並不是所有三角級數都是傅立葉級數。一個有趣的問題是給定一個三角級數,當x取什麼值時級數收斂。
基本介紹
- 中文名:三角級數
- 外文名:Trigonometric series
- 領域:數學
定義

唯一定理
傅立葉級數
歷史
定義




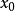



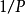







延伸

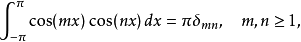

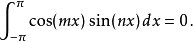
收斂性
- 在定義區間上,x(t)須絕對可積;
- 在任一有限區間中,x(t)只能取有限個極值點;
- 在任何有限區間上,x(t)只能有有限個第一類間斷點。

參閱
- 離散時間傅立葉級數
- 維爾斯特拉斯逼近定理
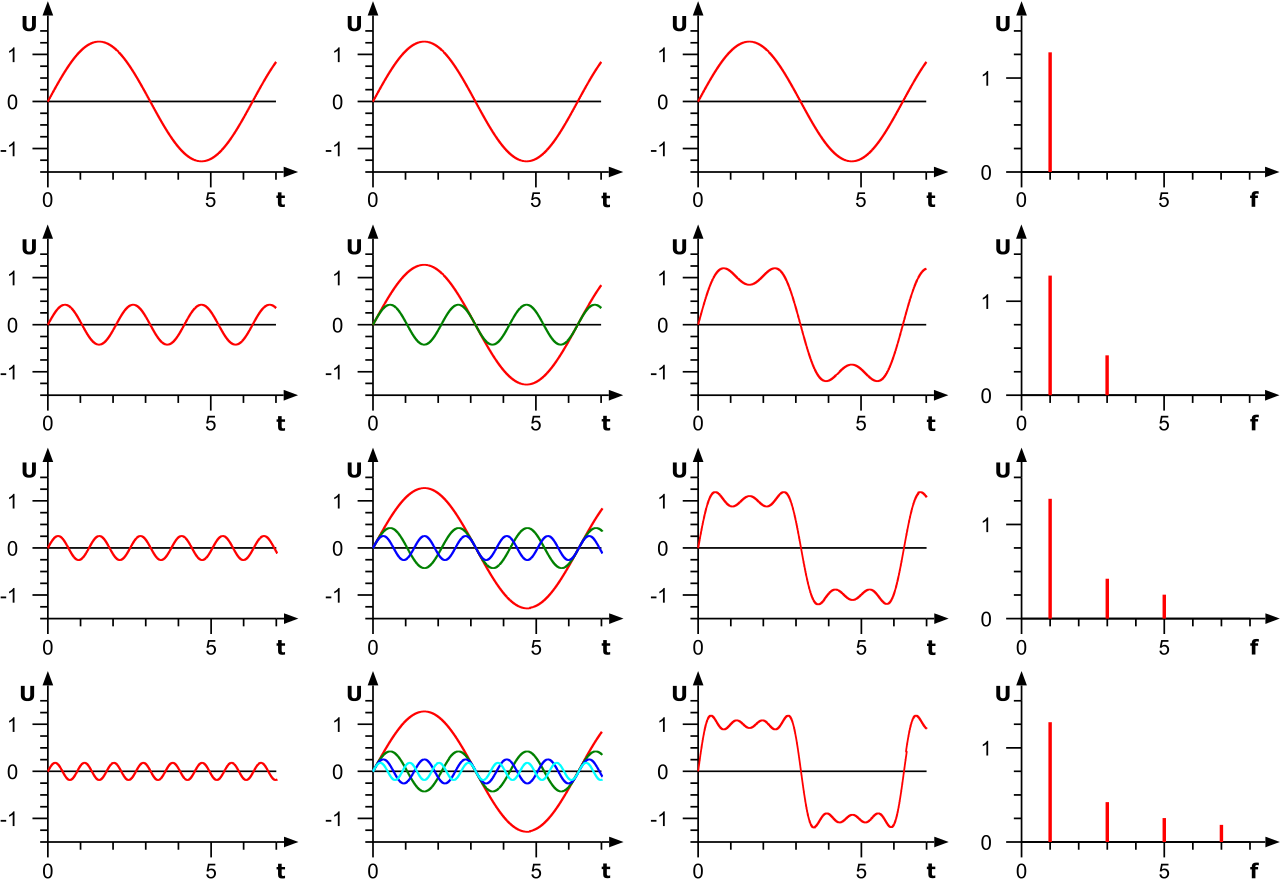
在數學中,傅立葉級數是一種三角級數,傅立葉級數也常稱為三角級數。但並不是所有三角級數都是傅立葉級數。一個有趣的問題是給定一個三角級數,當x取什麼值時級數收斂。





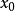



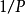








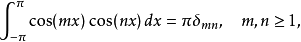

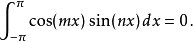

在數學中,傅立葉級數是一種三角級數,傅立葉級數也常稱為三角級數。但並不是所有三角級數都是傅立葉級數。一個有趣的問題是給定一個三角級數,當x取什麼值時...
《三角級數論(下冊)》是作者三十多年來為國內外研究生講授三角級數論所用講義幾經修改補充整理而成。全書共四章:第五章至第八章。第五章傅立葉級數的發散,...
《三角級數論(上冊)》是2012年12月哈爾濱工業大學出版社出版的圖書,作者是陳建功。...... 《三角級數論(上冊)》是作者三十餘年來為研究生講授三角級數論所用講義...
法國數學家傅立葉發現,任何周期函式都可以用正弦函式和餘弦函式構成的無窮級數來表示(選擇正弦函式與餘弦函式作為基函式是因為它們是正交的),後世稱傅立葉級數為一...
傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數。...... 傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數...
正交級數,即傅立葉級數。在數學中,傅立葉級數(Fourier series, /ˈfɔərieɪ/)是把類似波的函式表示成簡單正弦波的方式。更正式地說,它能將任何周期...
敘述了萊布尼茨三角形產生的歷史和萊布尼茨使用其創立微積分及在數學上作出的貢獻。...
三角函式是數學中屬於初等函式中的超越函式的函式。它們的本質是任何角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的。其定義...
《級數與拉普拉斯變換》是2003年9月化學工業出版社出版的圖書,作者是韓志剛。...... 一、周期函式與三角級數 37二、三角函式系的正交性 38三、周期為2的函式...
傅立葉展開式(Fourier expansion)是指用三角級數表示的形式,即一個函式的傅立葉級數在它收斂於此函式本身時的一種稱呼。若函式f(x)的傅立葉級數處處收斂於f (...
然而傅立葉的工作意義遠不止此,它迫使人們對函式概念作修正、推廣,特別是引起了對不連續函式的探討;三角級數收斂性問題更刺激了集合論的誕生。因此,《熱的解析...
在數學分析中,勒貝格定理,或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。這個定理有兩種形式,分別是關於周期函式(傅立葉理論中關於傅立葉級數的方面)和關於在...
